
赤ワインデータの解析

赤ワインデータの解析
統計解析、データ解析や機械学習に関する実データにもとづいた解析事例集です。ここでは、Rにより解析します。Rのスクリプトと結果(部分)はこのページの最後にリンクがあります。
解析する上で重要なことは、データについてよく理解することです。さらに、グラフや分析結果で何か特徴が見つかったら、それがその分野の知識と照らし合わせて、問題がないかどうか検討することが必要です。
解析の流れは以下のようになります。
 |
|
 |
 |
 |
 |
|||||||
| テキストファイル入力 | 散布図 |
回帰分析 |
主成分分析 による分類 |
SVM による分類 |
決定木 による分類 |
ランダム フォレスト |
まず、データについてよく理解します。
このデータセットは、ポルトガルの "Vinho Verde"ワインの赤い亜種に関連しています。詳細については、参考文献[Cortez
et al.,2009]を参照してください。プライバシーと物流の問題のため、物理化学的(入力)変数と官能的(出力)変数のみが利用可能です(例えば、ブドウの種類、ワインのブランド、ワインの販売価格などに関するデータはありません)。
CSV形式のデータは以下のところからダウンロードすることができます。
winequality-red2.csv
UC Irvine Machine Learning Repositoryは、カリフォルニア大学アーバイン校が運営,機械学習やデータマイニングに関するデータを配布しています。
https://archive.ics.uci.edu/ml/datasets/Wine+Quality
ここではアルファベットで変数名を定義します。
| 変数 | 変数名 | 説明 |
| 固定酸性度 | fixed_acidity | 固定酸度ワインに含まれるほとんどの酸は不揮発性(すぐに蒸発しない)。 |
| 揮発性酸性度 | volatile_acidity | 揮発性の酸度ワイン中の酢酸の量は、多すぎると不快な酢の味になる可能性があります。 |
| クエン酸 | citric_acid | クエン酸が少量の場合、ワインに「新鮮さ」と「風味」を加えることができます。 |
| 残留糖 | residual_sugar | 残留糖発酵が停止した後に残っている砂糖の量については、1グラム/リットル未満のワインと45グラム/リットルを超えるワインが甘いとみなされるのは稀です。 |
| 塩化物 | chlorides | |
| 遊離二酸化硫黄 | free_sulfur_dioxide | 微生物の成長とワインの酸化を防ぎます |
| 総二酸化硫黄 | total_sulfur_dioxide | 低濃度では、二酸化硫黄はワインではほとんど検出されませんが、50 ppmを超える遊離二酸化硫黄濃度では、ワインの香りや味に二酸化硫黄がはっきりと現れます。 |
| 密度 | density | 水の密度は、アルコールと糖分の割合によって、水の密度に近くなります。 |
| pH | ph | ほとんどのワインはpHが3-4の間です。 |
| 硫酸塩 | sulphates | 抗菌剤および酸化防止剤として寄与することができるワイン添加物 |
| アルコール | alcohol | ワインのアルコール含有量 |
| 品質 | quality | 官能データに基づいて、0から10の間のスコア |
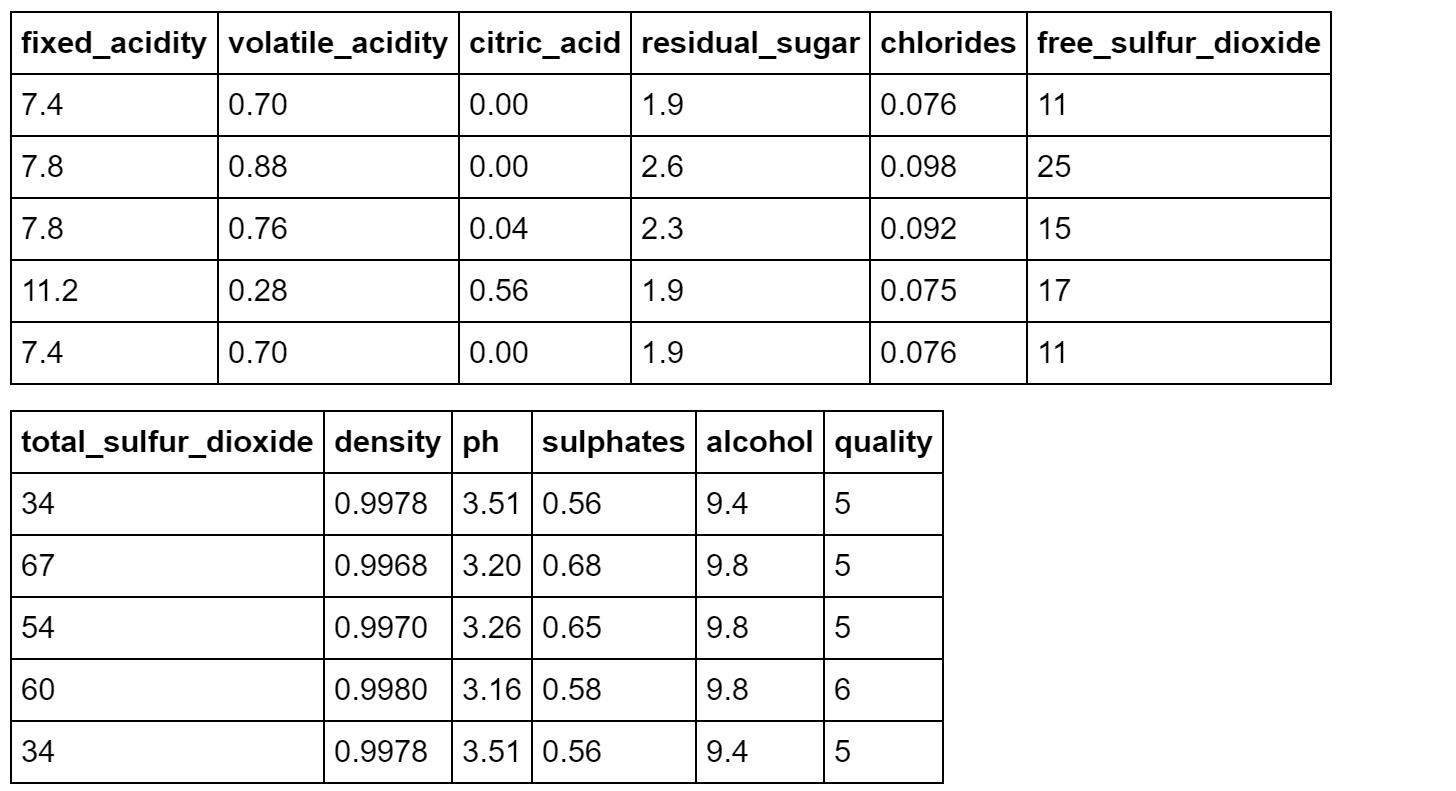
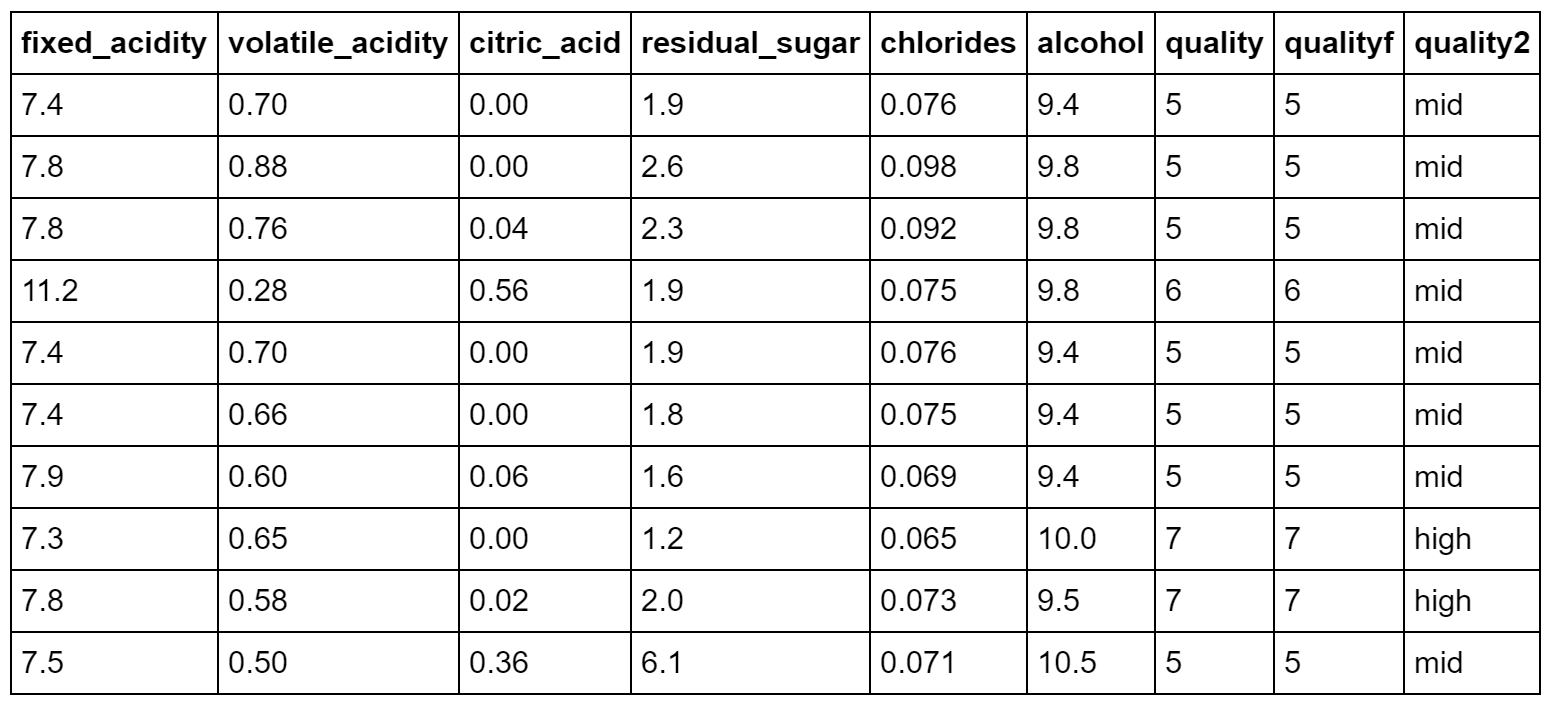
以下にデータの最初の5件を表示します。
多変量解析や機械学習により、どの物理化学的特性がワインを「良くする」のかを判断します。
参考文献:
P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis. Modeling wine preferences by data mining from physicochemical properties.
In Decision Support Systems, Elsevier, 47(4):547-553, 2009.
ここから参照することができます。
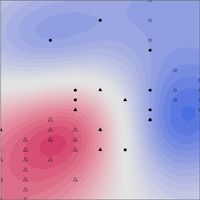
散布図は連続量の変数に対して求めます。ここでは、品質qualityはカテゴリ量で、それ以外の変数は連続量ですが、品質と他の変数との関係を調べてみます。
揮発性酸性度volatile_acidityと品質との関係は、品質が高いほど揮発性酸性度の値は小さくなるように見えます。
塩化物chloridesと品質との間には関係がないように見えます。

上の図とその他の変数の散布図(RあるいはPythonのスクリプトと結果を参照してください)から、外れ値のような観測値を除いて解析することにします。具体的には、以下のようなスクリプトで除きます。例えば、揮発性酸性度volatile_acidityは1.2よりも大きな観測値を除きます。
wine_quality_red2<-wine_quality_red[wine_quality_red$volatile_acidity<1.2
& wine_quality_red$chlorides <0.5
& wine_quality_red$total_sulfur_dioxide<200
& wine_quality_red$ph<3.8
& wine_quality_red$sulphates<1.5
& wine_quality_red$alcohol<14
& wine_quality_red$fixed_acidity<15
& wine_quality_red$citric_acid<0.9
& wine_quality_red$residual_sugar<9
& wine_quality_red$free_sulfur_dioxide<55
& wine_quality_red$density<1.002,]
品質qualityはカテゴリ量で、3から8の間の値を取っています。連続量ではありませんが、値には順序関係があるので、連続量として扱ってみます。品質を目的変数として、他の変数を説明変数として回帰分析で解析してみます。
回帰分析は、説明変数の情報を利用して目的変数の値を予測する手法です。
目的変数:回帰式を使って予測する変数で、従属変数ともよばれます。
説明変数:目的変数を予測する際に使用する変数で、独立変数ともよばれます。 一般に、目的変数の値を予測するための式として、目的変数の一次式(線型式)が用いられます。
y = a0 + a1 x1 + a2 x2 + ..... + ap xp
この式を回帰式とよび、a0,a1,a2,….,apをデータから推定するパラメータで、a0を定数項、a1,a2,….,ap?を回帰係数といいます。各パラメータは、最小2乗法により推定されます。具体的には、観測値と予測値との差(残差)の2乗和を最小にするようにパラメータの値を決めます。下のデータによる回帰モデルは以下のように表されます。左辺が目的変数、右辺が説明変数です。
quality = a0 + a1 fixed_acidity + a2 volatile_acidity + ..... + a11 alcohol
参考文献:山口和範、よくわかる統計解析の基本と仕組み、秀和システム
まず、品質quality以外の11個の変数を説明変数として解析します。決定係数は0.3727とあまりよくありません。

説明変数ごとのt検定で有意にならなった変数を除いてみます。
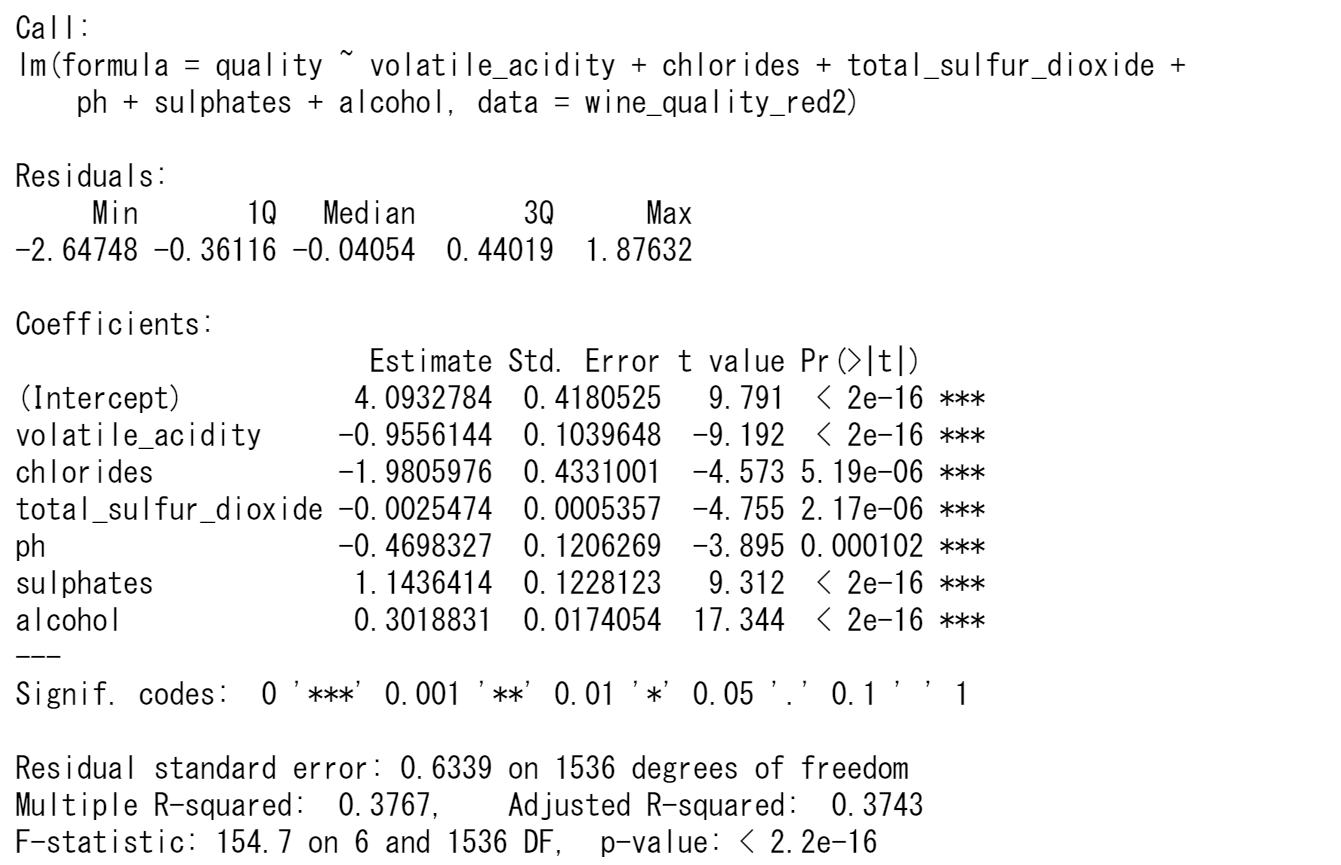
決定係数はよくありませんが、品質qualityと関係がある変数は以下のものです。
揮発性酸性度volatile_acidity
塩化物chlorides
総二酸化硫黄total_sulfur_dioxide
pH ph
硫酸塩sulphates
アルコールalcohol
残差と予測値の散布図などは以下のとおりです。
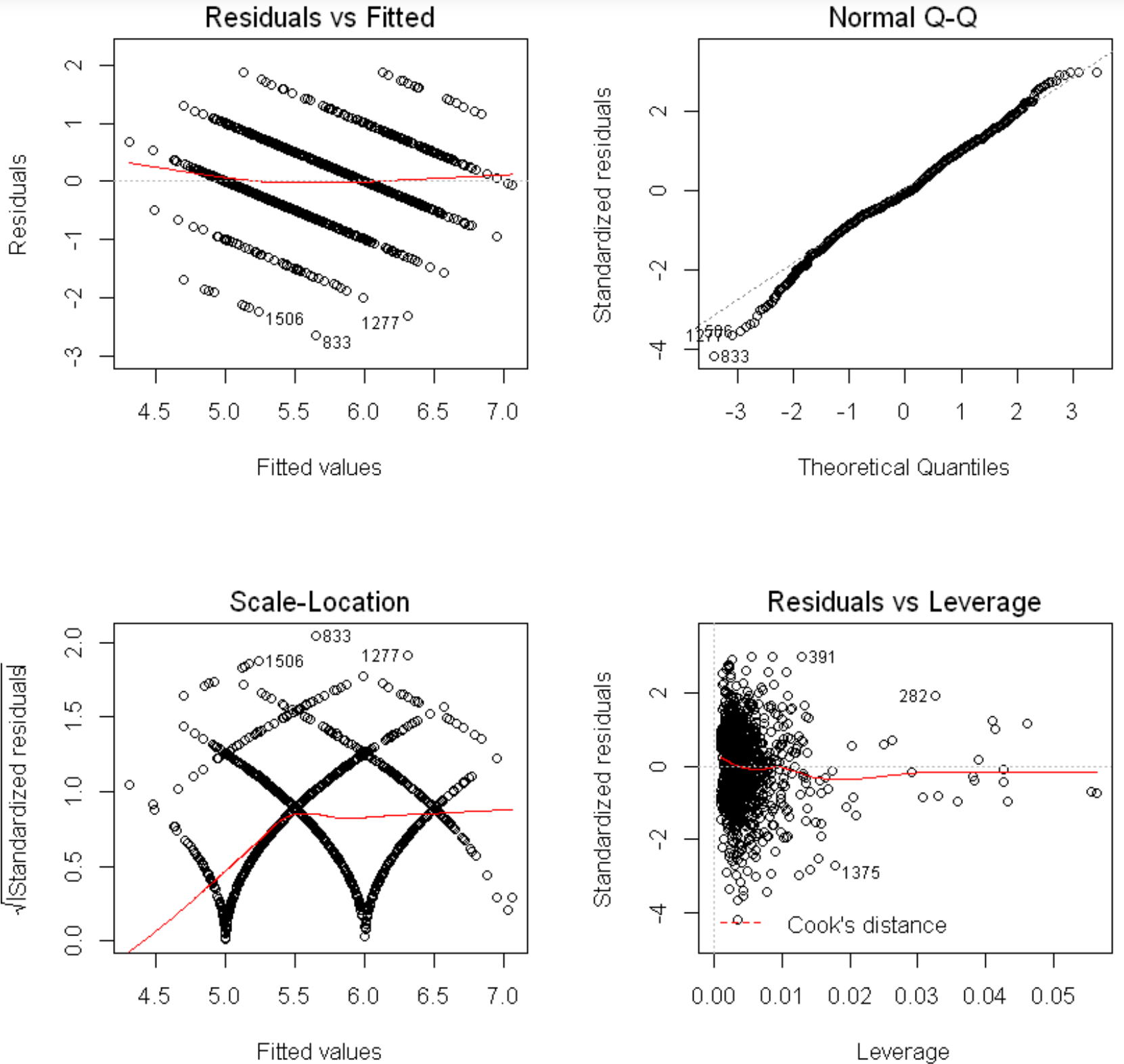
決定係数が低いので回帰モデルとしては適切ではありませんが、後の解析でこの結果を参考にします。
品質qualityも含めてすべての変数を主成分分析で解析して、変数間の関係を調べてみます。
主成分分析とは、多くの変数の値を、1個または少数個の総合的指標(主成分)に代表させようという手法です。これにより、多くの変数を持つデータを、少ない次元で表すことができ、変数や観測値の分類なども可能になります。
変数x1,x2,...xp に対して任意の係数(ak1,ak2,...,akp),k=1,2,..m,m≦pを用いて、以下のようなp変数の一次結合を作ります。x1,x2,...xp は連続量の変数です。
z1=a11x1+a12x2+...+a1pXp
z2=a21x1+a22x2+...+a2pXp
:
zm=am1x1+am2x2+...+ampXp
係数aを次の条件を満足するように定めます。
条件1:(ak1)2+(ak2)2+...+(akp)2=1
条件2:第1主成分の係数a11,a12,...,a1pは、z1の分散が最大になるように定めます。
条件3:第k主成分の係数ak1,ak2,...,akpは、
zkが、z1,...,zk-1と無相関になるように定めます。
上の条件を満たすように係数aを求めるには、相関係数行列または分散共分散行列から固有値・固有ベクトルを計算することになります。一般的には、変数の単位の違いをなくすために相関係数行列から計算します。求まった固有ベクトルが係数aになります。各z1、z2、...が、それぞれ第1主成分、第2主成分、...となります。
固有値の大きさにより、各主成分の情報量が分かります。相関係数行列から計算した場合、p個の固有値の合計はpになるので、固有値をpで割ることにより寄与率が計算されます。
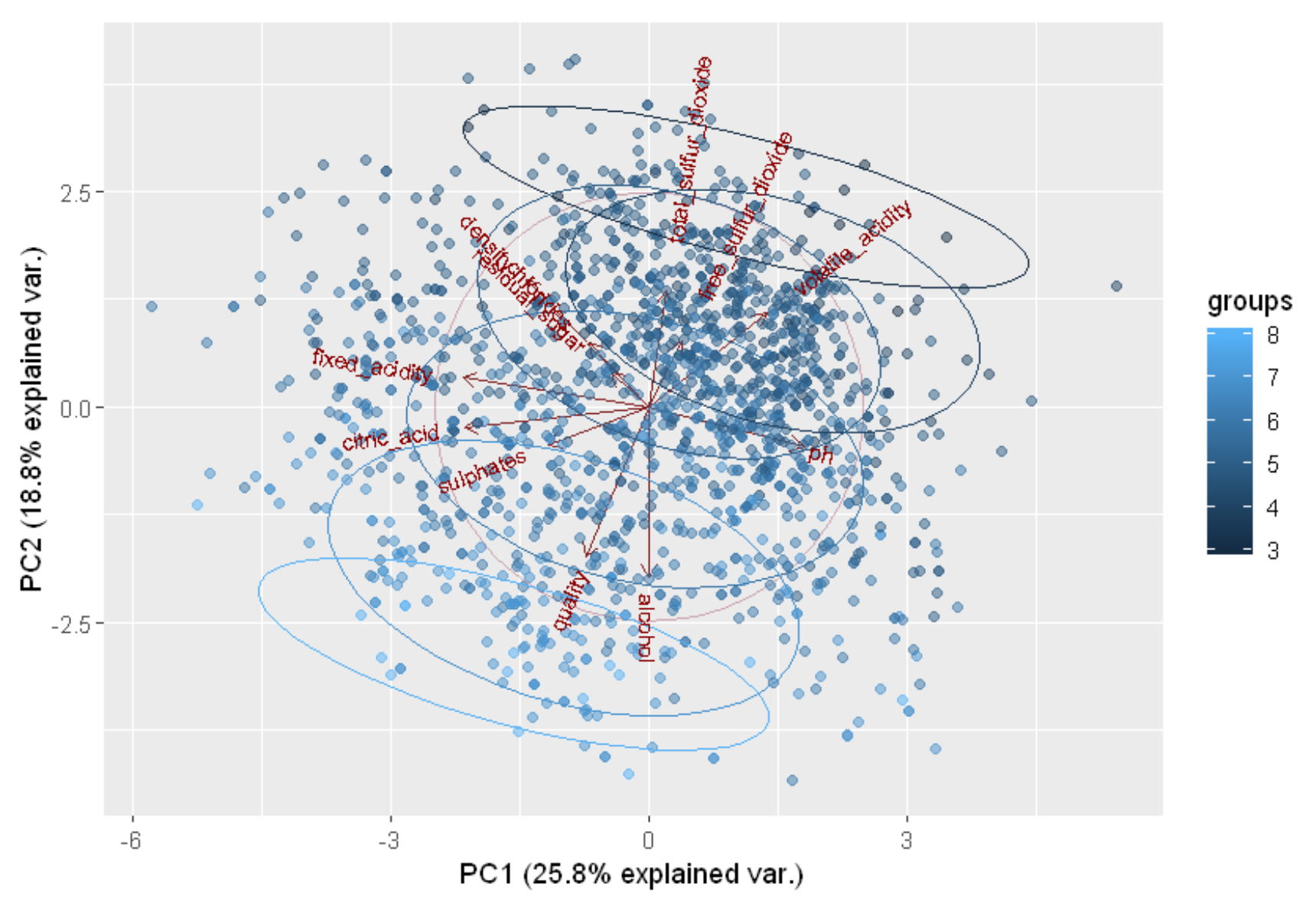
まず、固有値と固有ベクトルは以下のとおりです。主成分は元の変数の個数だけ求まりますが、ここでは固有ベクトルは第5主成分まで表示します。固有値により各主成分の寄与の度合いが分かります。この場合、第1主成分は25.8%(3.0967÷12)の寄与率があります。つまり、第1主成分は全体の情報量の25.8%を占めています。
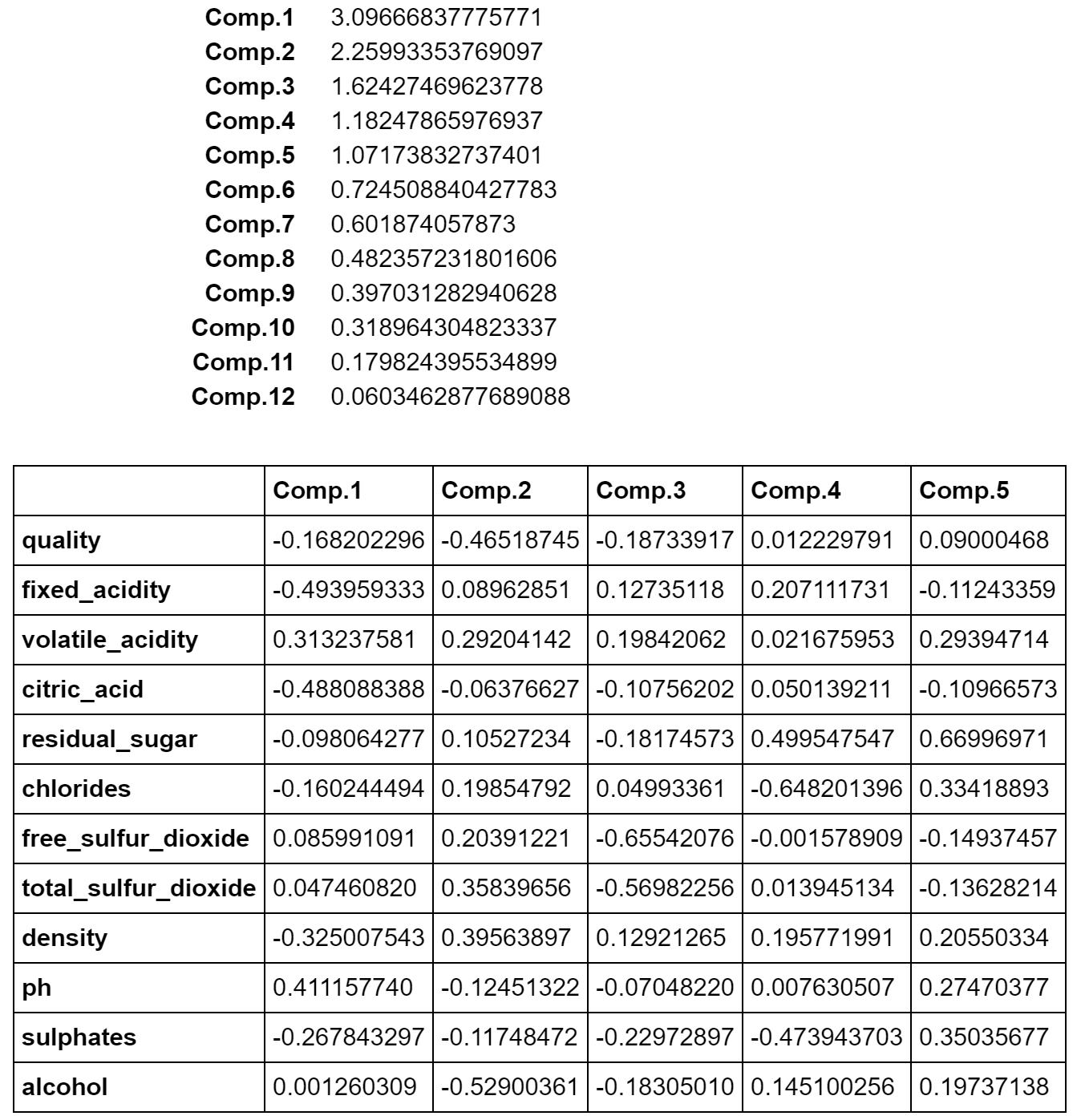
つぎは、主成分と元の変数との相関である主成分負荷量です。
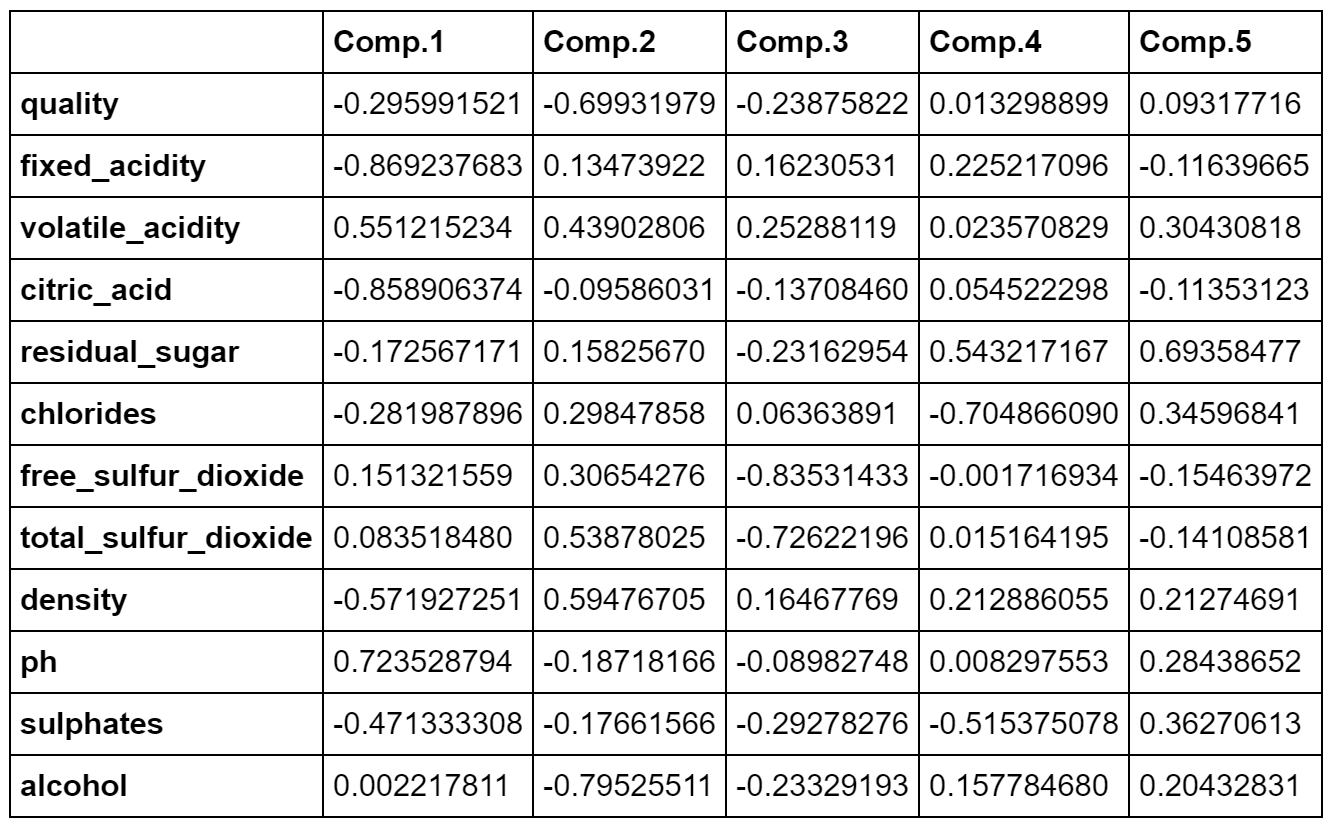
主成分負荷量のプロットを見ると変数間の関係が分かります。以下は、第1主成分と第2主成分のプロットです。
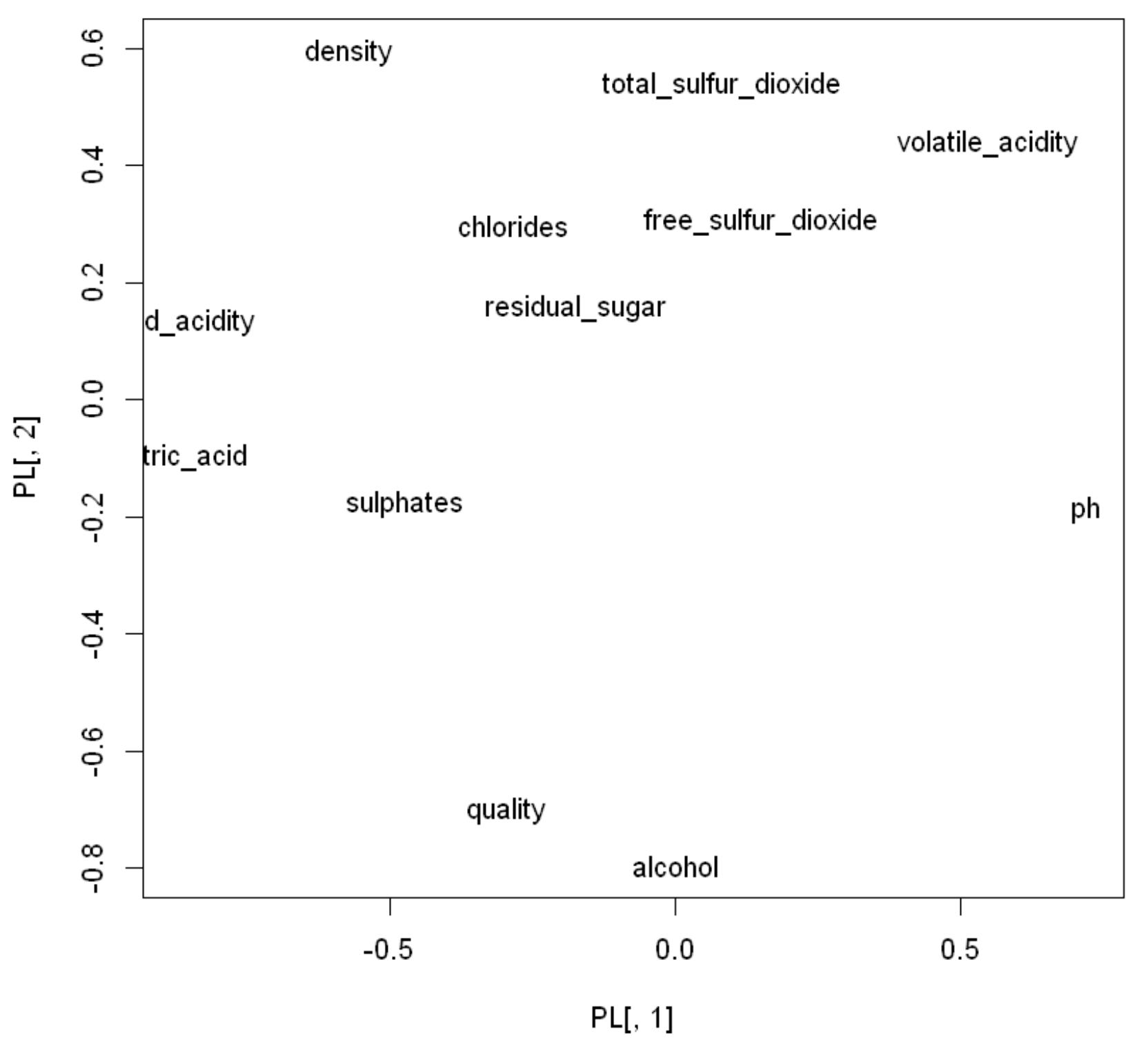
主成分を軸として、変数の因子負荷量と、観測値ごとの主成分スコアをプロットしたバイプロットを見てみます。これを見ると、品質qualityとアルコールalcoholが近い関係にあります。また、第2主成分(y軸)方向に品質の高い方が下、品質の低い方が上の方に分布していることが分かります。
サポートベクターマシンは下図左に示すように、直線や平面などで線形分離できないデータを、高次元の空間に写像して線形分離することにより、分類/回帰を行う手法です。実際は、高次元の空間に写像するのではなく、データ間の近さを定量化する「カーネル」(高次元の空間でのデータ間の内積に相当)を導入しています。
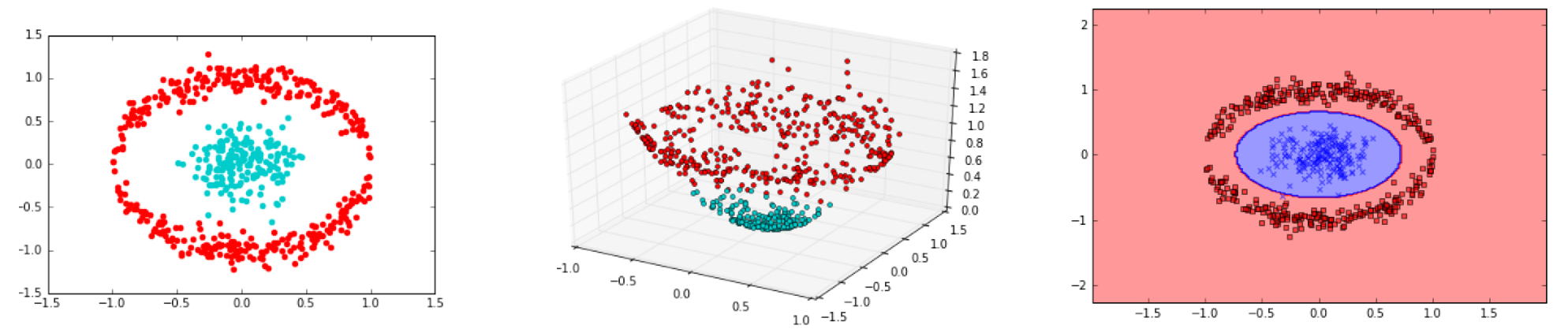
この例では、以下の射影により、2次元のデータセットを新しい3次元の特徴空間に変換し、クラスを分離します。
Φ(x1,x2)=(x1,x2)=(x1,x2,x12+x22)
2次元のデータセット(図左)を射影Φにより3次元のデータセット(図中)に変換することにより、2つのクラスを線形超空間を使って分離できるようになります。それを元の特徴空間へ射影すると、非線形の決定境界(図右)になります。
参考文献:S. Raschka著、福島真太郎監訳、Python機械学習プログラミング、インプレス
Rサポーターズ、パーフェクトR、技術評論社
ワインの品質を10段階に分けて予測をするのは難しいようです。大半が中程度のもので、品質の高いものや低いものの件数が少ないことも原因です。このため、品質を3段階にして、分類の問題にしてみます。
low:1~4
mid:5~6
high:7~10
変換したデータは以下のようになります。
品質quality2を目的変数、残りの固定酸性度~アルコールを説明変数としてSVMで解析します。精度は0.866となりましたが、lowをlowとして予測できた件数が0でした。カーネルはrbfです。

回帰分析の結果を参考にして、説明変数を減らしてみます。カーネルはrbfです。
揮発性酸性度volatile_acidity
塩化物chlorides
総二酸化硫黄total_sulfur_dioxide
pH ph
硫酸塩sulphates
アルコールalcohol

精度は前とあまり変わりませんが、lowをlowとして予測できた件数が2になりました。
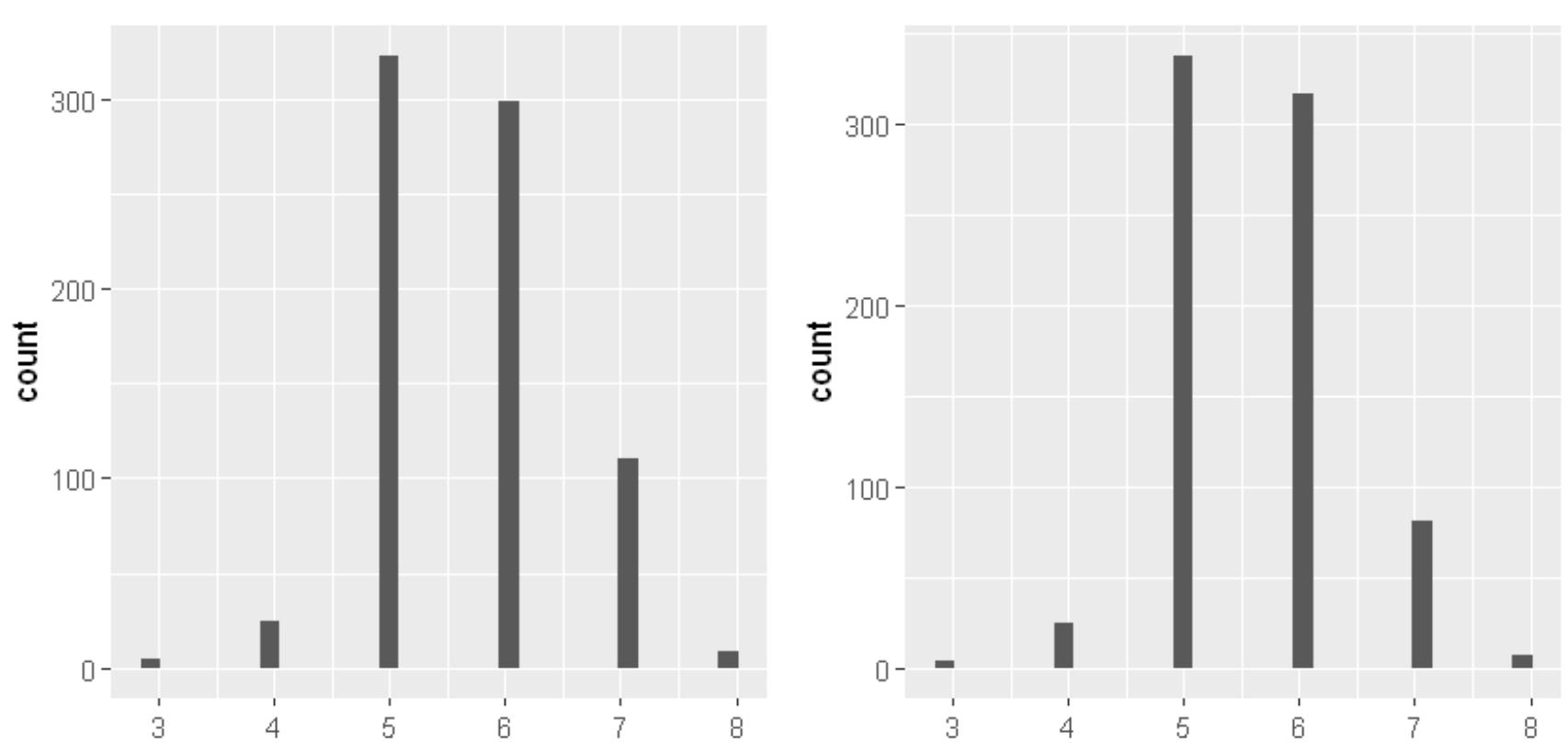
今度は、データ全体を学習データとテストデータに分けて解析し、SVMモデルが予測に使えるかどうか確認してみます。ここでは、学習データとテストデータを1:1に分割します。それぞれ771件と772件です。学習データとテストデータの分布を見てみます。
SVMの結果は以下のようになります。カーネルはrbfで、説明変数は減らした6個です。精度の結果は、上が学習データ、下がテストデータです。lowをlowと予測できていないのは問題ですが、前の結果とあまり変わりません。

決定木ではラベルつきデータ(x1,y1),…., (xn,yn),が観測されたとき、木構造の推論規則を用いて入力xに対するラベルyを予測します。ここで、木構造とは下図のように枝分かれしていくグラフ構造を指します。
データx=(x1,…,xn)∈Rdに対して、根ノードから出発し、各ノードにある条件に従って葉に向かって進んでいきます。葉に割り当てられたラベルがxに対する予測値です。各ノードでの条件は、典型的には、x∈Rdのある要素xk (k∈{1,….,d})と実数cに対して「xk>cを満たすかどうか」という形式で記述されます。この条件に従って、次に進むノードが決まります。すなわち、xの各要素に対するif-thenルールの組み合わせによって、最終的なラベル予測を行います。このような推論規則を決定木(もしくは分類木)といいます。
決定木の学習では、判別、回帰の両方の問題に対してほとんど同じアルゴリズムを適用できるため、汎用的な手法として広く用いられています。さらに、各ノードで単純なルールに従って入力空間が分割されるため、学習された規則を解釈しやすいという利点があります。一方、予測精度はあまり高くありません。
参考文献:金森敬文、Rによる機械学習入門、オーム社
ここでは、品質qualityを目的変数、他の変数を説明変数として分類します。
データ全体を学習データとテストデータとして1:1に分割して分析します。決定木の結果は、Rのものです。Pythonでの結果はRの場合と異なりますが、データを学習データとテストデータとランダムに分割した結果が異なるためです。
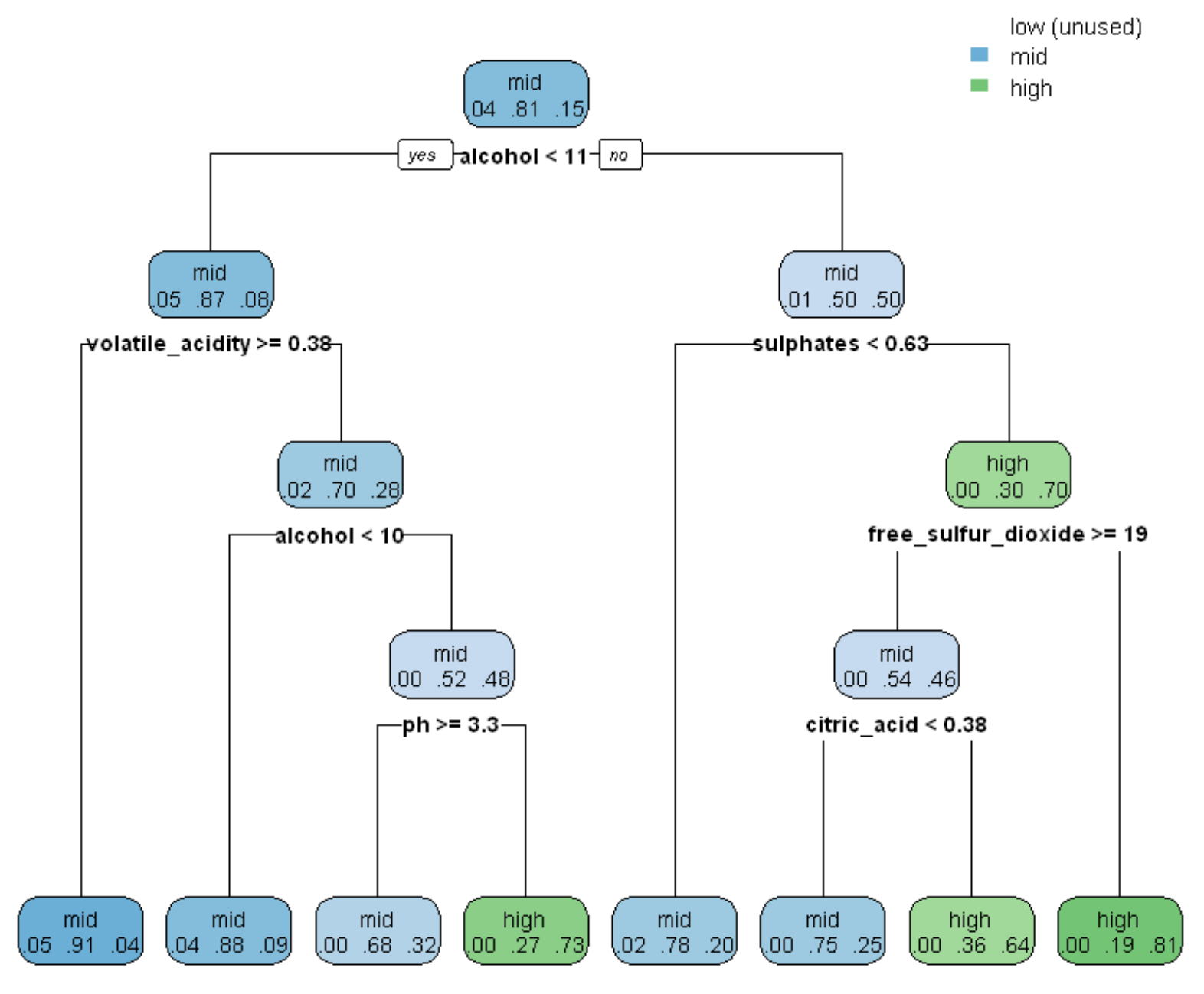
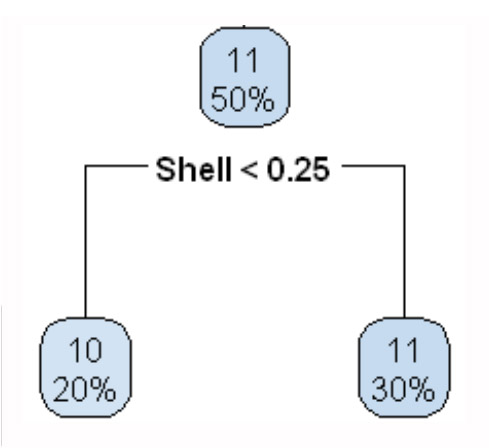
決定木の結果をグラフに表示しましたが、以下のように解釈できます。
・最初、全体(学習データ)を、alcoholが11未満かどうかで分けます。
このとき、品質がlowは4%、midが81%、highが15%です。
・左側(alcohol<11)では、揮発性酸性度volatile_acidityが0.38以上かどうかで分けます。
このとき、品質がlowは5%、midが87%、highが8%です。
・右側では、硫酸塩sulphatesが0.63未満かどうかで分けます。
このとき、品質がlowは0%、midが30%、highが70%です。
決定木の精度を学習データとテストデータのそれぞれの場合で求めます。


ランダムフォレストは、データの特徴量(説明変数)をランダムに選択して決定木を構築する処理を複数回繰り返し、各木の推定結果の多数決や平均値により分類・回帰を行う手法です。ランダムに選択されたサンプルと特徴量(説明変数)のデータをブートストラップデータと呼びます。ランダムフォレストは決定木のアンサンブル(集合)であり、このように複数の学習器を用いた学習方法をアンサンブル学習とよびます。
参考文献:寺田学ほか、Pythonによるデータ分析の教科書、翔泳社
品質qualityを目的変数、他の変数を説明変数として分類します。データ全体を学習データとテストデータとして1:1に分割して分析します。

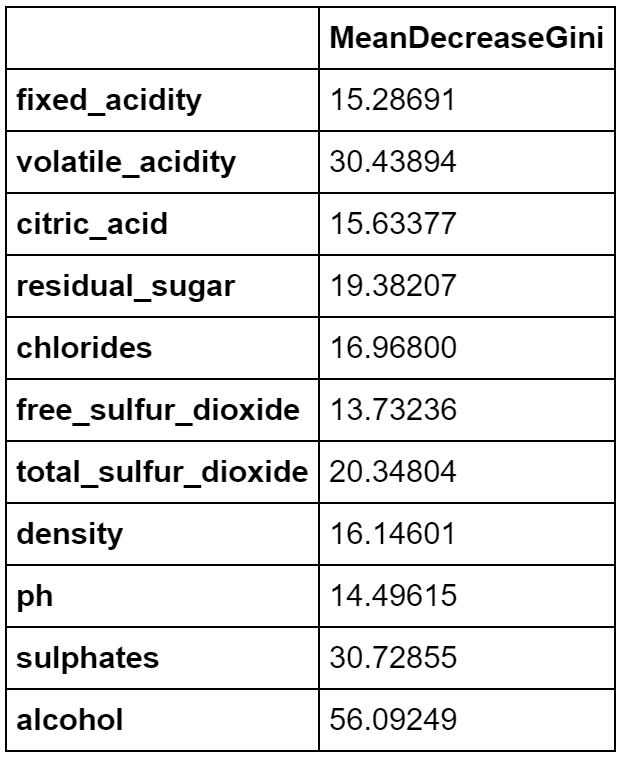
各変数の重要度も表示することができます。アルコールalcohol、揮発性酸性度volatile_acidity、硫酸塩sulphatesの重要度が高いようです。
以下はテストデータに対する精度です。

redwine01_python.htm
redwine01_R.html
スクリプトと結果は一部分です。全体はセミナーのときに紹介します。
イラストについて は、下記のサイトのイラスト素材を用いています。
無料でイラスト素材のダウンロード!【イラストAC】
Copyright © 2019 株式会社スタットラボ All Rights Reserved.《Web Design:Template-Party》