
心臓病データの解析

心臓病データの解析
統計解析、データ解析や機械学習に関する実データにもとづいた解析事例集です。RやPythonなどのスクリプトと結果(部分)はこのページの最後にリンクがあります。
解析する上で重要なことは、データについてよく理解することです。さらに、グラフや分析結果で何か特徴が見つかったら、それがその分野の知識と照らし合わせて、問題がないかどうか検討することが必要です。

解析の流れは以下のようになります。
 |
|
|
|
|
 |
|||||
| テキストファイル 入力 |
散布図と 相関係数 |
回帰分析 による予測 |
判別分析 による分類 |
ロジスティック回帰分析 | 決定木 |
まず、データについてよく理解します。
データについては、heart01での情報を参照してください。変数とサンプル、カテゴリ量と連続量、データの出典などについてです。
CSV形式のデータは以下のところからダウンロードすることができます。
heart2.csv
ここではアルファベットで変数名を定義します。
| 変数 | 変数名 | 説明 |
| 年齢 | age | 年齢(歳) |
| 性別 | sex | 1 =男性、0 =女性 |
| 胸痛タイプ | cp | 胸痛タイプ - 1:典型的な狭心症 typical angina - 2:非定型狭心症 atypical angina - 3:非狭心症性の痛み non-anginal pain - 4:無症状 asymptomatic |
| 安静時血圧 | trestbps | 入院時mm Hg |
| 血清コレステロール | chol | mg/dl |
| 空腹時血糖値 | fbs | 空腹時血糖値>120 mg/dl : 1 =真、0 =偽 |
| 安静時心電図結果 | restecg | - 0:通常 normal - 1:ST-T波異常(T波の反転および/またはSTの上昇または下降>0.05 mV) having ST-T wave abnormality - 2:エステスの基準による左心室肥大の可能性または確定 showing probable or definite left ventricular hypertrophy by Estes' criteria |
| 最大心拍数 | thalach | 拍/分 |
| 運動誘発狭心症 | exang | 1 =はい、0 =いいえ |
| ST低下 | oldpeak | 安静時と比較して運動により誘発されたST低下 |
| STセグメントの勾配 (ピーク運動) |
slope | - 1:上昇 - 2:フラット - 3:下降 |
| 主要血管の数 | ca | 蛍光透視法で着色された、0-3 |
| 正常欠損区分 | thal | 3:正常 normal、6:固定性欠損 fixed defect、7:可逆性欠損 reversable defect |
| 心臓病の診断 | heart_disease | 0:正常(thal=3) 1:心臓病(thal=6 または 7) |
ここでは、正常と心臓病の人(変数:心臓病の診断)がいますが、その人たちの測定値にはどのような違いがあるのかを調べます。心臓病の場合は、6:固定性欠損と、7:可逆性欠損(変数:正常欠損区分)の2種類があります。
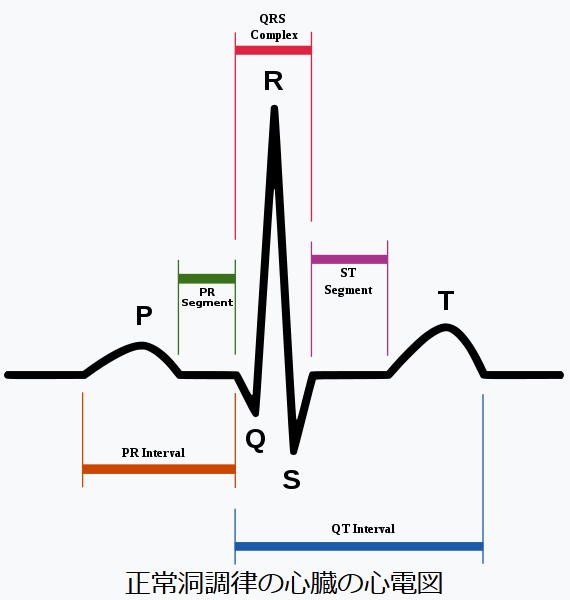
ウィキペディアを参照。
連続量の変数に対して散布図や相関係数を求めます。
連続量の変数は、年齢age、安静時血圧trestbps、血清コレステロールchol、最大心拍数thalach、ST低下oldpeakです。
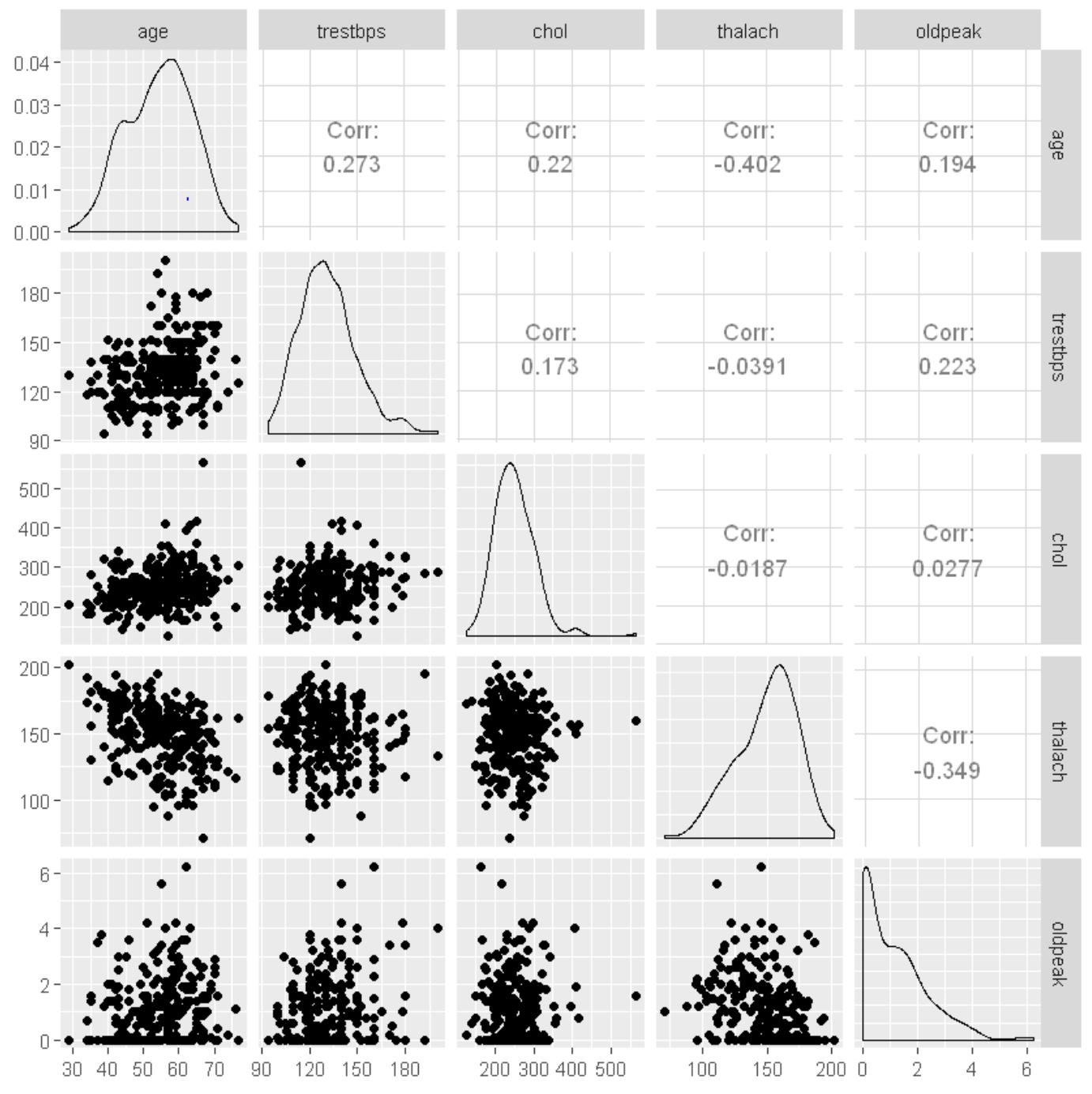
相関係数はー1から+1までの値を取ります。各変数間には高い相関はないようです。
ここでは、ST低下oldpeakを目的変数、他の変数を説明変数として予測します。
回帰分析は、説明変数の情報を利用して目的変数の値を予測する手法です。
目的変数:回帰式を使って予測する変数で、従属変数ともよばれます。
説明変数:目的変数を予測する際に使用する変数で、独立変数ともよばれます。 一般に、目的変数の値を予測するための式として、目的変数の一次式(線型式)が用いられます。
y=a0+a1x1+a2x2+...+apxp
この式を回帰式とよび、a0,a1,a2,….,apをデータから推定するパラメータで、a0を定数項、a1,a2,….,apを回帰係数といいます。各パラメータは、最小2乗法により推定されます。具体的には、観測値と予測値との差(残差)の2乗和を最小にするようにパラメータの値を決めます。下のデータによる回帰モデルは以下のように表されます。左辺が目的変数、右辺が説明変数です。
oldpeak=a0+a1age+a2sex+a3cp+...+a12thal
参考文献:山口和範、よくわかる統計解析の基本と仕組み、秀和システム
回帰分析の目的変数と説明変数は、連続量のデータです。ところが、性別、胸痛タイプ、空腹時血糖値、安静時心電図結果、運動誘発狭心症、などがカテゴリ量になります。これらの変数はダミー変数に変換してから扱います。
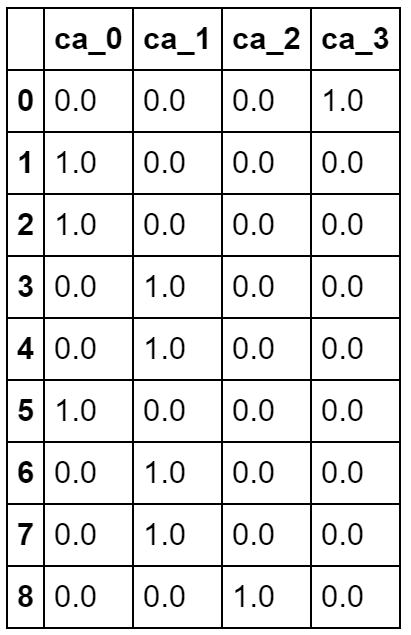
ダミー変数とはカテゴリ量データを0と1で表す変数です。一般にカテゴリ量のように値の大小によってパラメータに影響を与えない項目についてはダミー変数に変換して分析します。例えば、主要血管の数caでは0から3の4つの値を取ります。スクリプトはPythonによる例です。
heart_df5=heart_df[["ca"]] heart_df5.head(9)

新しくできた4つの変数(ca_0~ca_3)の値を合計すると常に1になり、行列が正則でなくなり回帰分析や判別分析などの計算ができなくなるため、4つの中の1つを使わずに分析します。
heart_df6=pd.get_dummies(heart_df5, drop_first=False, columns=['ca']) heart_df6.head(9)
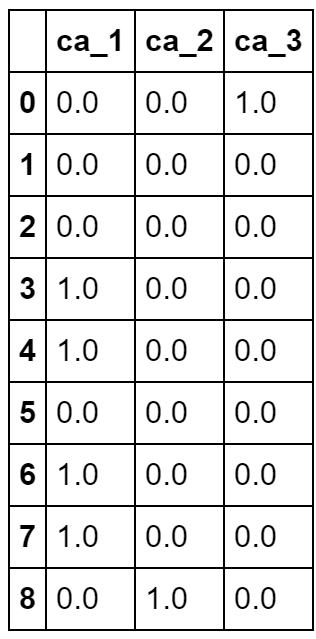
Pythonでは、get_dummies関数を用いて変換します。
heart_df5=heart_df[["ca"]] heart_df5.head(9)
Rでは、変数を関数as.factorを用いて因子にすることにより、回帰分析や判別分析の中で自動的にダミー変数に変換して処理してくれます。
ここでは、ST低下oldpeakに影響を与える要因について、回帰分析によって解析します。
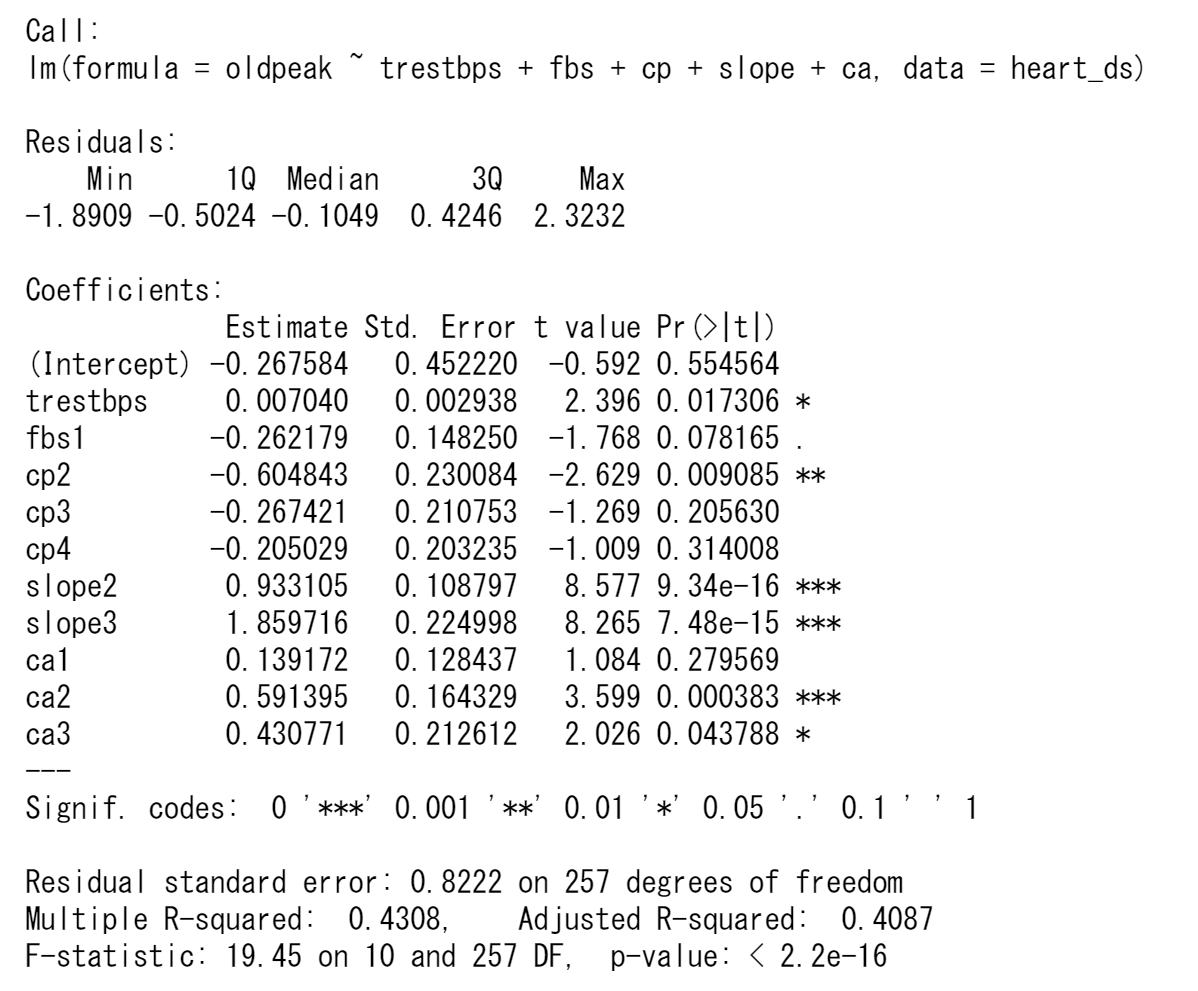
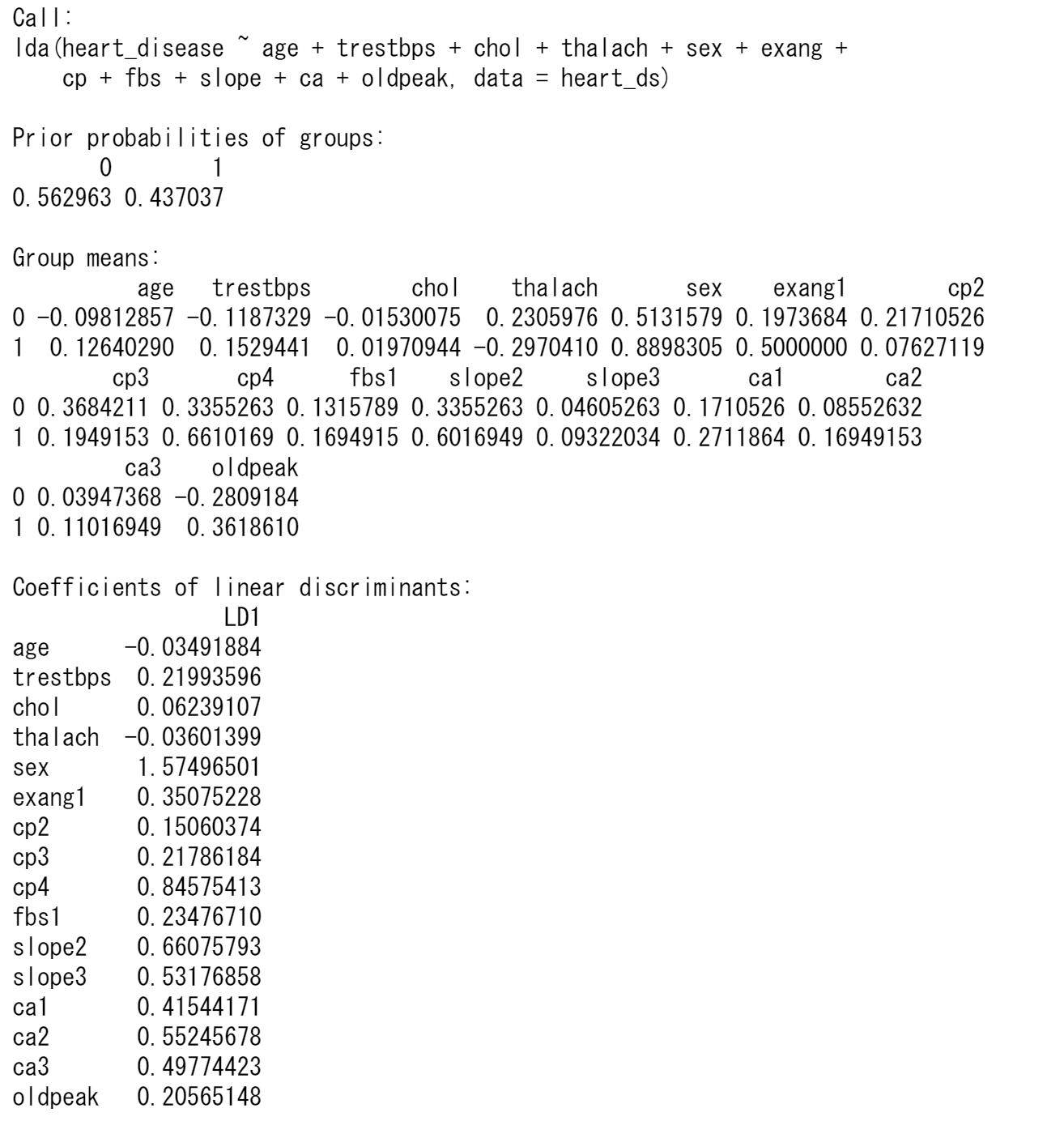
ST低下oldpeakを目的変数、残りのすべての変数を説明変数として回帰モデルを推定してみます。解析の結果は以下のようになります。
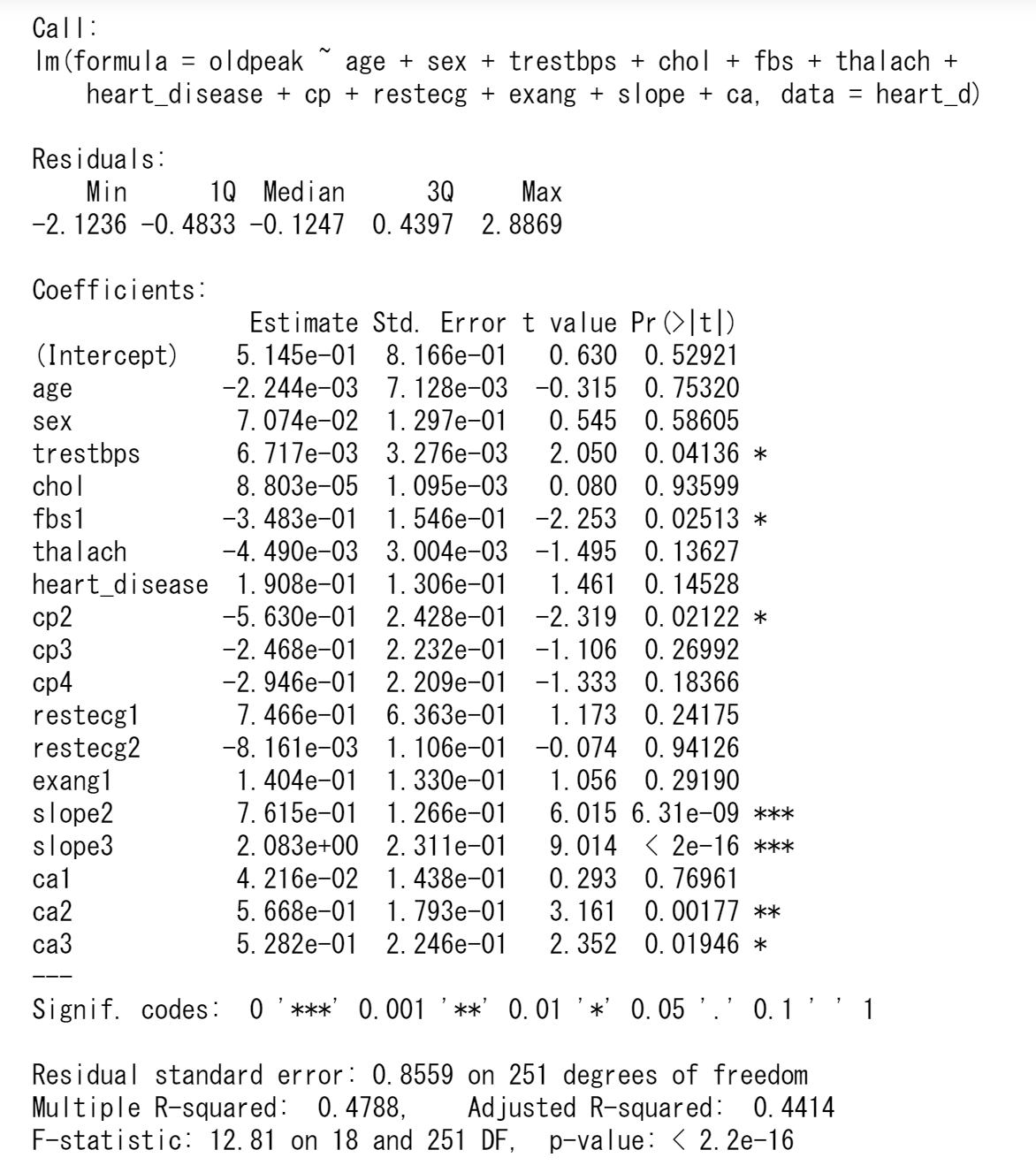
この場合の決定係数は0.4824であまり高くはありません。決定係数の平方根が重相関係数で0.6945となります。
説明変数の個数が多いので、t値とそのp値の大きさにより、説明変数の取捨選択をします。変数はなるべく少なく、決定係数R-squaredは1に近づくようにします。各回帰係数のt検定の結果で有意になっていない変数を除いて分析し直します。このとき、カテゴリ変数については、有意なものが1つでもあれば残りも入れておくことにします。

各説明変数は有意なものだけ残りました。決定係数は0.4392と前とあまり変わりません。回帰式は以下のようになります。
oldpeak=-0.7702+0.0084trestbps-0.3389fbs1+0.9817slope2+2.3118slope3+....
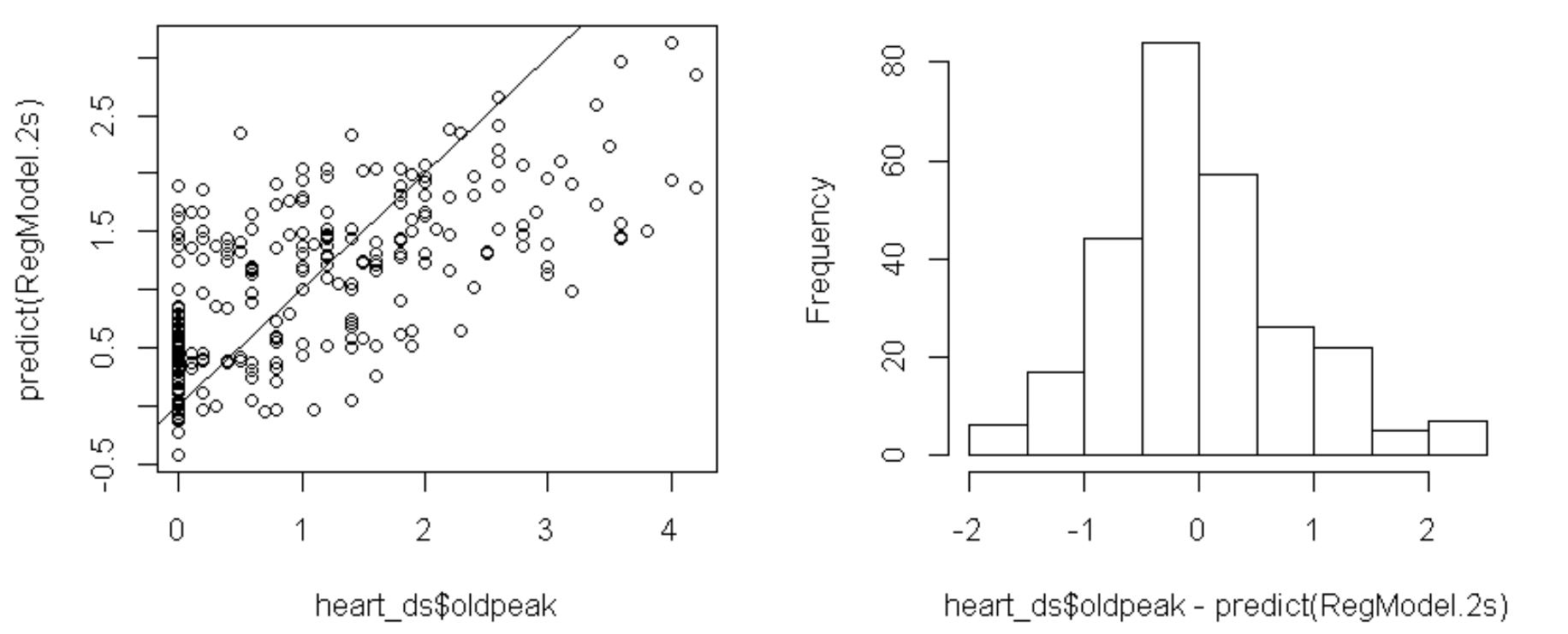
つぎに、残差の分布を見るなどの回帰診断を行ってみます。
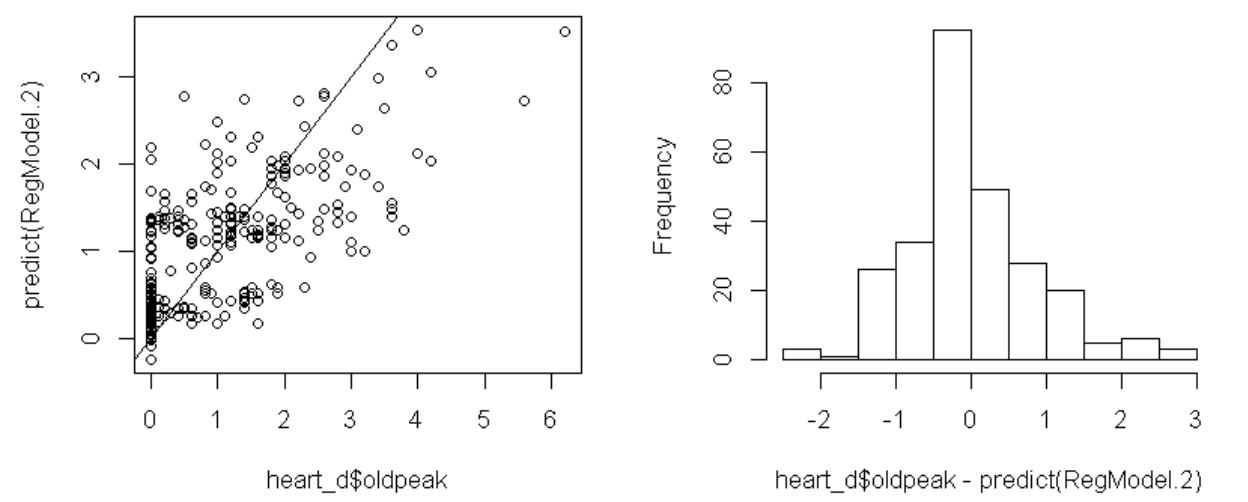
一番下の左ののグラフは、目的変数と目的変数の予測値との散布図ですが、oldpeakの値が5よりも大きな観測値が他よりも外れているようです。これらの2個の観測値を除いて分析してみます。
心臓病の診断heart_diseaseを目的変数、他の変数を説明変数として分類します。
事前に与えられた異なるグループのデータがあり、新しいデータが得られたときに、どのグループに入るのかを判別するための基準(判別関数)を得るための分類の手法です。判別関数は以下の式で表されます。
z=a0+a1x1+a2x2+...+apxp
まず、2変数ずつの散布図を描いてみます。データは回帰分析と同じものを使います。
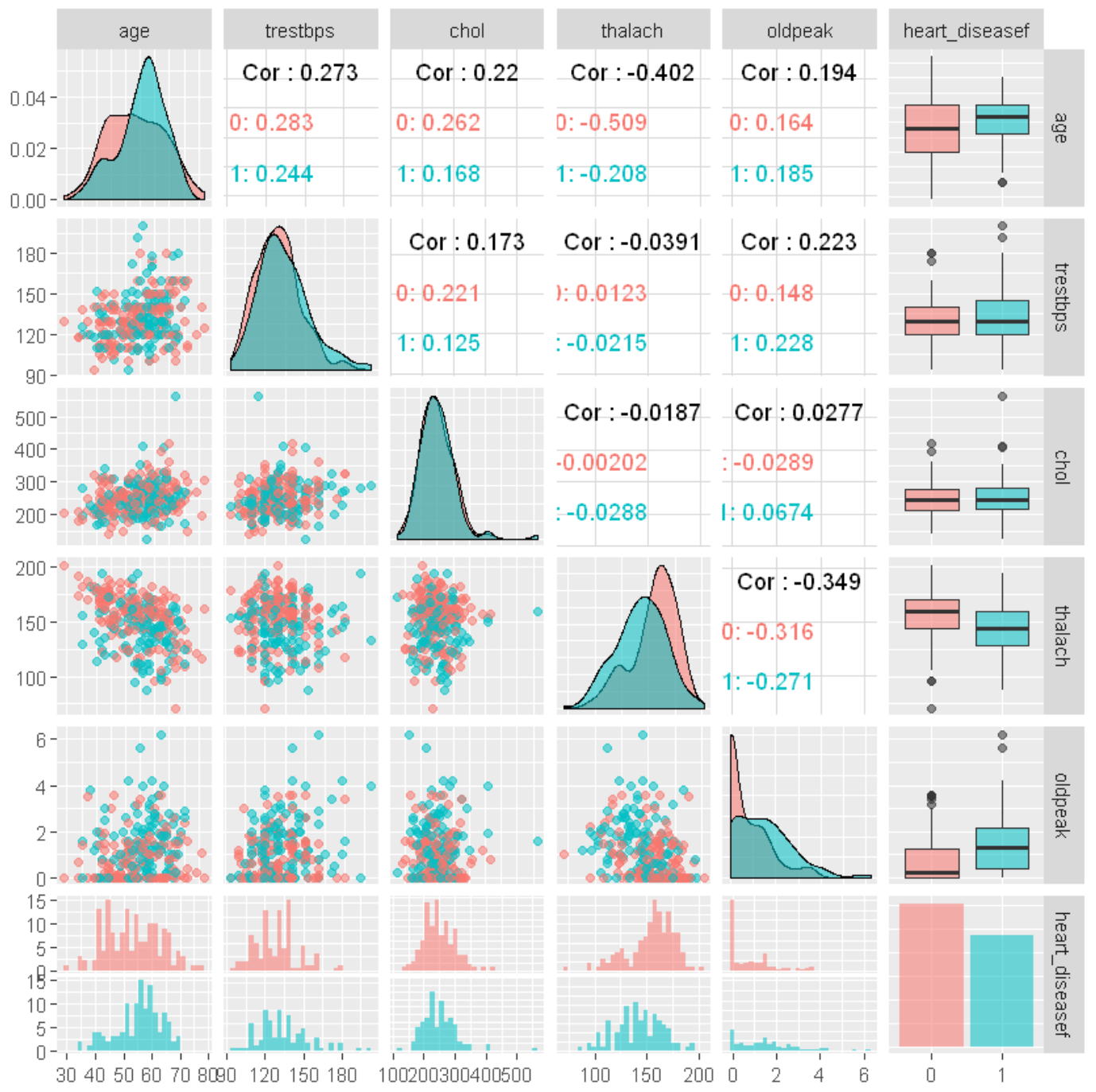
説明変数は連続量でなくてはならないため、回帰分析のときと同じように、カテゴリ変数はダミー変数に変換します。
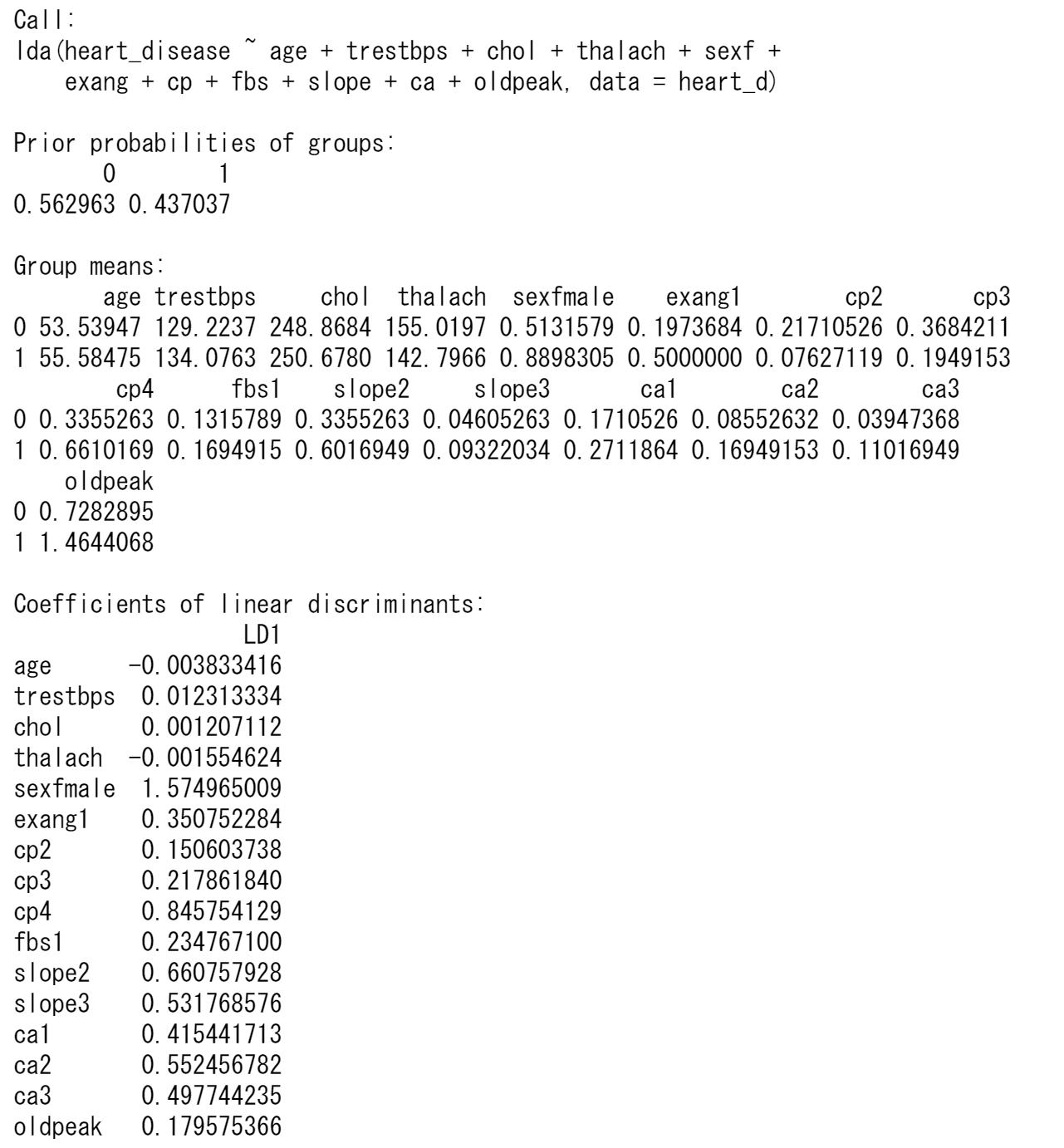
心臓病の診断heart_diseaseを目的変数、他の変数を説明変数として分類します。heart_diseaseは0または1の値をとり、2つのグループになります。
判別関数の係数の計算は固有値・固有ベクトルの計算になり、固有ベクトルが係数になります。以下を参照してください。
https://tgmstat.wordpress.com/2013/12/12/reduced-rank-discriminant-analysis/
上はRの結果ですが、Pythonの場合は係数の値が異なります。固有ベクトルは定数倍したものも同じ固有ベクトルです。Rの結果とPythonの結果を比較すると係数は定数倍になっていますので、どちらも正しい値です。
判別分析では、回帰分析のときのように各係数の検定結果が表示されないため、どの変数が有意なのか分かりません。そのため、各変数を標準化(平均0、標準偏差1にする)したときの判別関数の係数値の大きさにより、どの変数が判別関数に寄与しているか判断することにします。連続量の変数を標準化して、判別分析をやり直します。
この判別関数のコンフュージョンマトリックスと精度を計算します。

上の結果から、ここでは判別係数の絶対値が0.3より大きな変数を選択してみます。
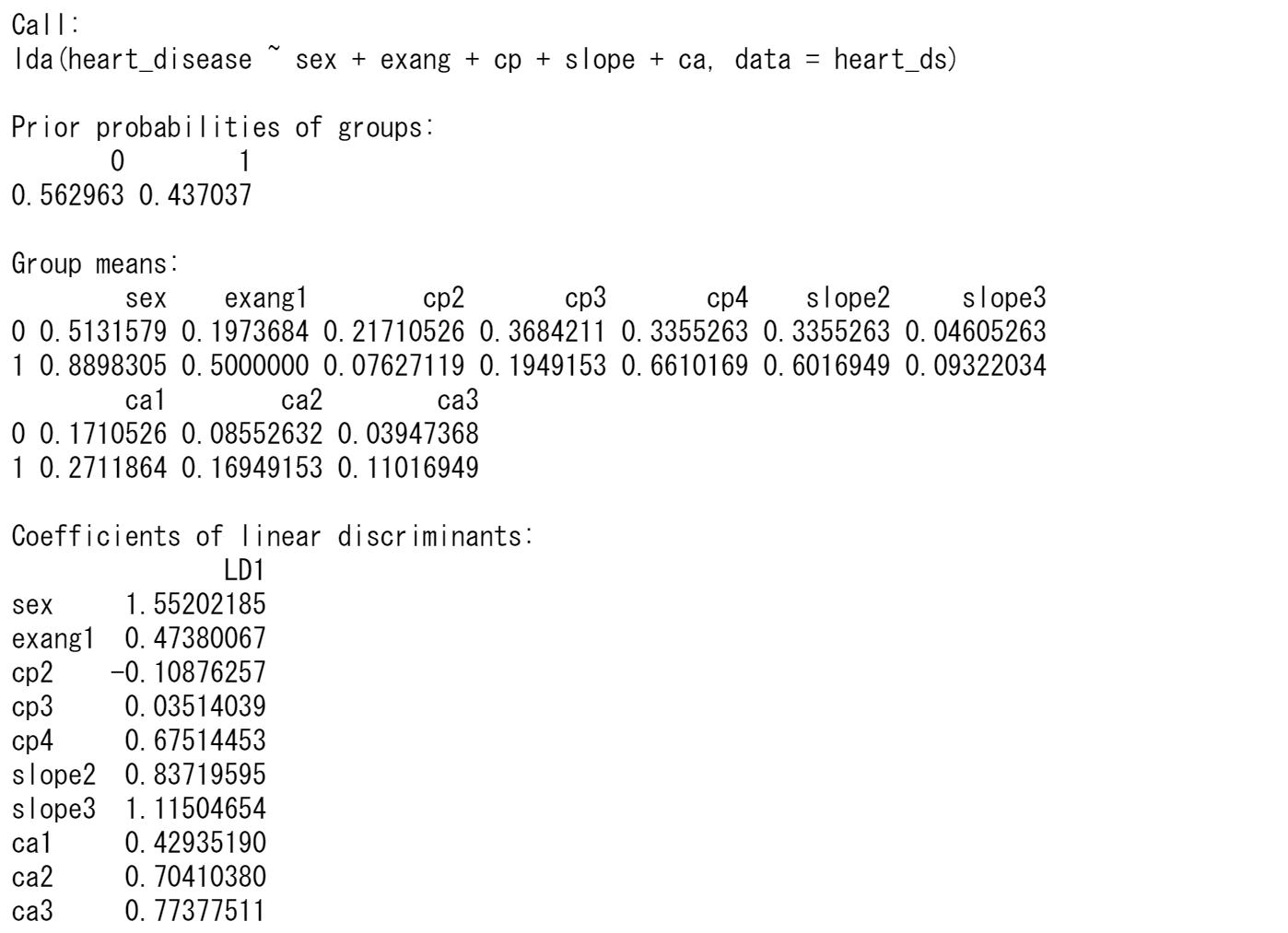
判別関数の定数項は判別係数とグループの平均値から求めることができ、この場合は、2.2968になります。判別関数は以下のような式になります。
z=2.2968+1.552sex+0.4738exang1-0.1087cp2+0.0351cp+30.6751cp4+....
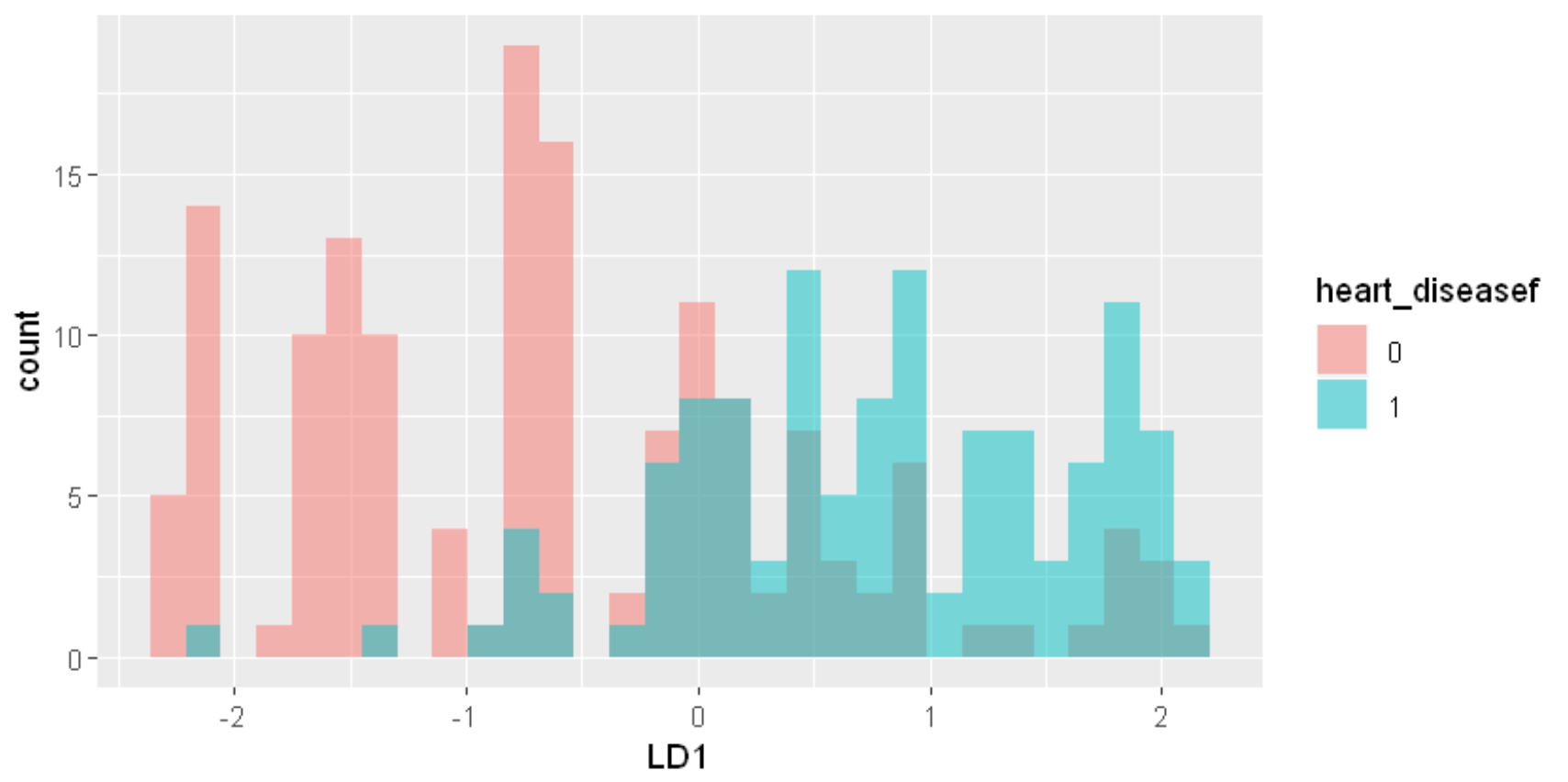
この判別関数のコンフュージョンマトリックスと精度を計算します。

変数を減らす前と精度はほとんど変わりません。判別スコアのヒストグラムを描いてみると、コンフュージョンマトリックスでみたように、かなり誤判別があることが分かります。
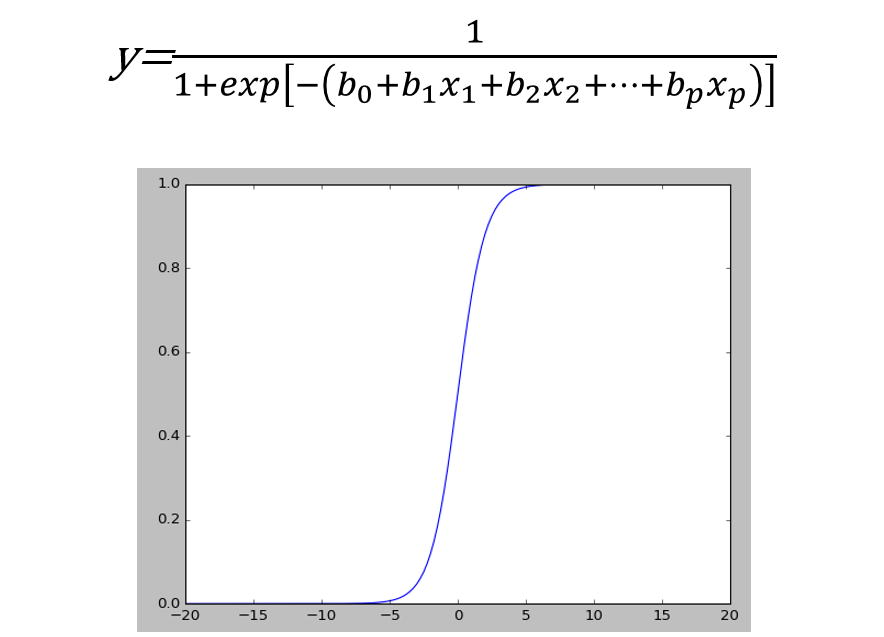
ロジスティック回帰は確率を予測したり、2クラスに分類する手法として使われており、予測結果が0から1の間、もしくは0か1を取るように数式やその前提に改良が加えられています。
ロジスティック回帰モデルは以下の式のように表され、各xを説明変数として、目的変数yは0から1の間の値をとります。
ここでは、心臓病の診断heart_diseaseを目的変数、他の変数を説明変数として分類します。
説明変数でカテゴリ量のものは、ダミー変数に変換します。

ここでは、学習データ(3/4)とテストデータ(1/4)に分けて分析します。学習データにより推定されたロジスティック回帰モデルは以下のようになります。
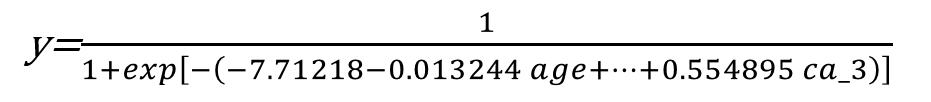

オッズ比 (odds ratio) とは、ある確率が起こる確率 p と起こらない確率 1-p との比です。下の式の左辺を、 𝑝(𝒙)の1−𝑝(𝒙)に対するオッズ比と言います。
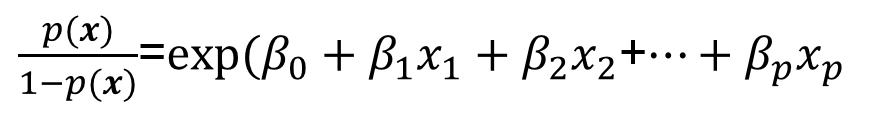
オッズ比とロジスティック回帰係数βの関係は以下のようになります。
オッズ比=exp(𝛽𝑖)
説明変数𝑥𝑖が1だけ変化するとき、目的変数はexp(𝛽𝑖)倍変化します。
各変数のオッズ比を比べることにより、モデルに寄与している大きさを判断できます。

変数を整理して、モデルを推定しなおしてみます。

コンフュージョンマトリックスと精度を、学習データとテストデータそれぞれで出してみます。


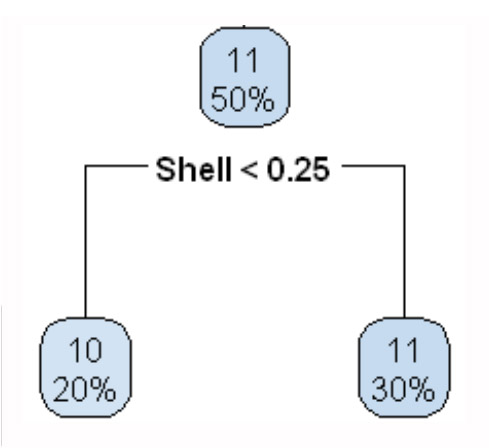
決定木はラベルつきデータ(x1,y1),…., (xn,yn),が観測されたとき、木構造の推論規則を用いて入力xに対するラベルyを予測します。ここで、木構造とは下図のように枝分かれしていくグラフ構造を指します。
データx=(x1,…,xn)∈Rdに対して、根ノードから出発し、各ノードにある条件に従って葉に向かって進んでいきます。葉に割り当てられたラベルがxに対する予測値です。各ノードでの条件は、典型的には、x∈Rdのある要素xk (k∈{1,….,d})と実数cに対して「xk>cを満たすかどうか」という形式で記述されます。この条件に従って、次に進むノードが決まります。すなわち、xの各要素に対するif-thenルールの組み合わせによって、最終的なラベル予測を行います。このような推論規則を決定木(もしくは分類木)といいます。
決定木の学習では、判別、回帰の両方の問題に対してほとんど同じアルゴリズムを適用できるため、汎用的な手法として広く用いられています。さらに、各ノードで単純なルールに従って入力空間が分割されるため、学習された規則を解釈しやすいという利点があります。一方、予測精度はあまり高くありません。
参考文献:金森敬文、Rによる機械学習入門、オーム社
心臓病の診断heart_diseaseを目的変数、他の変数を説明変数として分類します。決定木では、カテゴリ変数をダミー変数に変換する必要はありません。
変数heart_diseaseは、変数thalの3を0、6と7を1に変換しているので、thalも説明変数から除きます。
データを学習データとテストデータとして3:1に分割して分析します。Rでは、各変数の重要度も表示することができます。決定木の結果は、Rのものです。Pythonでの結果はRの場合と異なりますが、データを学習データとテストデータとランダムに分割した結果が異なるためです。

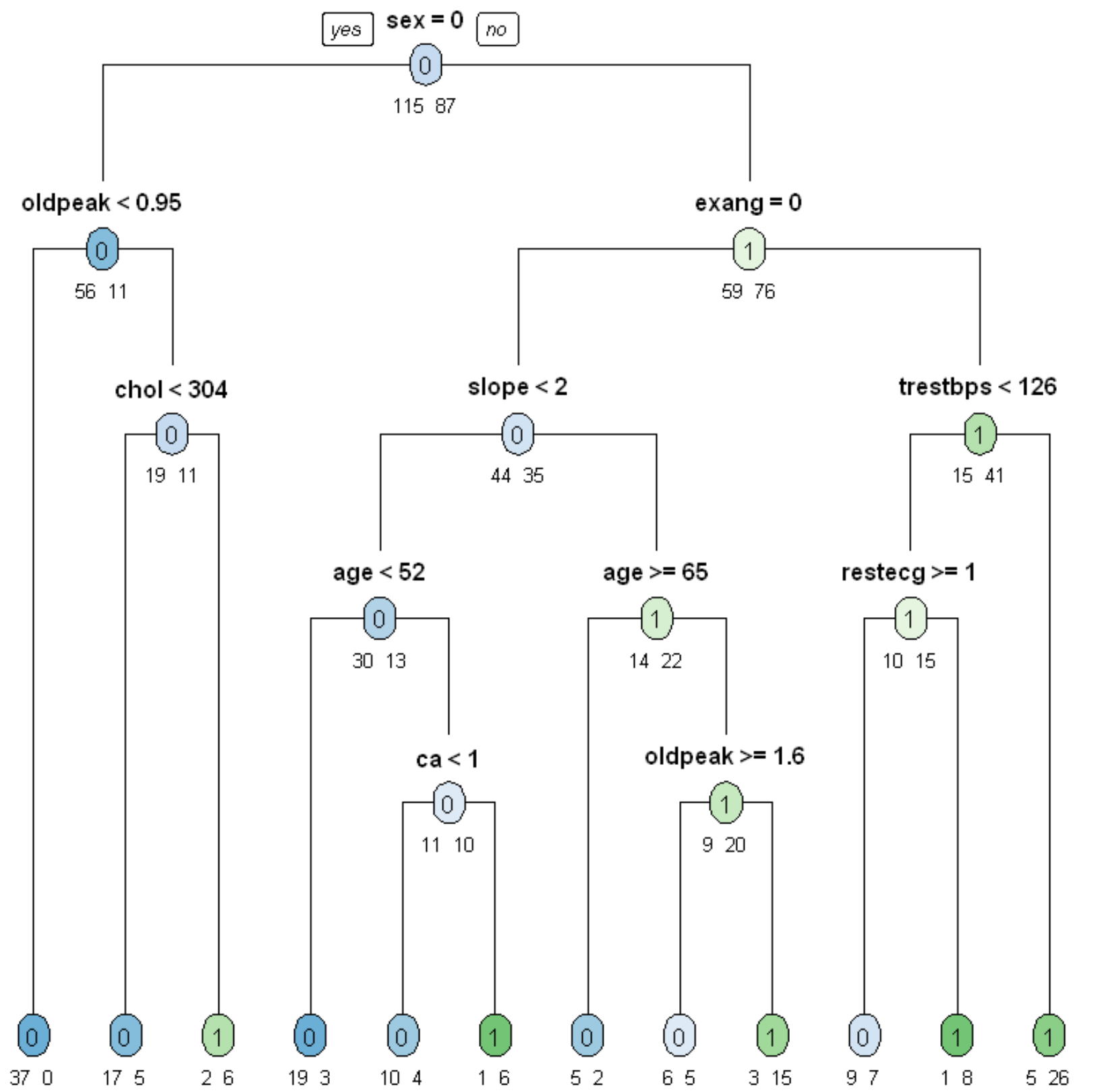
決定木の結果をグラフに表示します。
・最初、全体で202人(学習データ)で、性別が女性が67人で男性が135人です。
このとき、heart_diseaseの0が115人、1が87人です。
・女性67人の中、ST低下(oldpeak)が0.95以下は37人、0.95より大は30人です。
このとき、heart_diseaseの0が56人、1が11人です。
・135人の中、最大心拍数(exang)が0は79人、1は56人です。
このとき、heart_diseaseの0が59人、1が76人です。
決定木による予測をテストデータで行います。

heart02_python.html
heart02_R.html
スクリプトと結果は一部分です。全体はセミナーのときに紹介します。
イラストについて は、下記のサイトのイラスト素材を用いています。
写真・イラスト・動画素材販売サイト【PIXTA(ピクスタ)】
無料でイラスト素材のダウンロード!【イラストAC】
Copyright © 2019 株式会社スタットラボ All Rights Reserved.《Web Design:Template-Party》