データ解析・機械学習解析事例集

心臓病データの解析：グラフや平均値の差の検定、分散分析による解析です。

まず、データについてよく理解します。

データ解析におけるデータは、列方向が変数（項目）、行方向がサンプル（観測値）である2次元の行列で表されます。

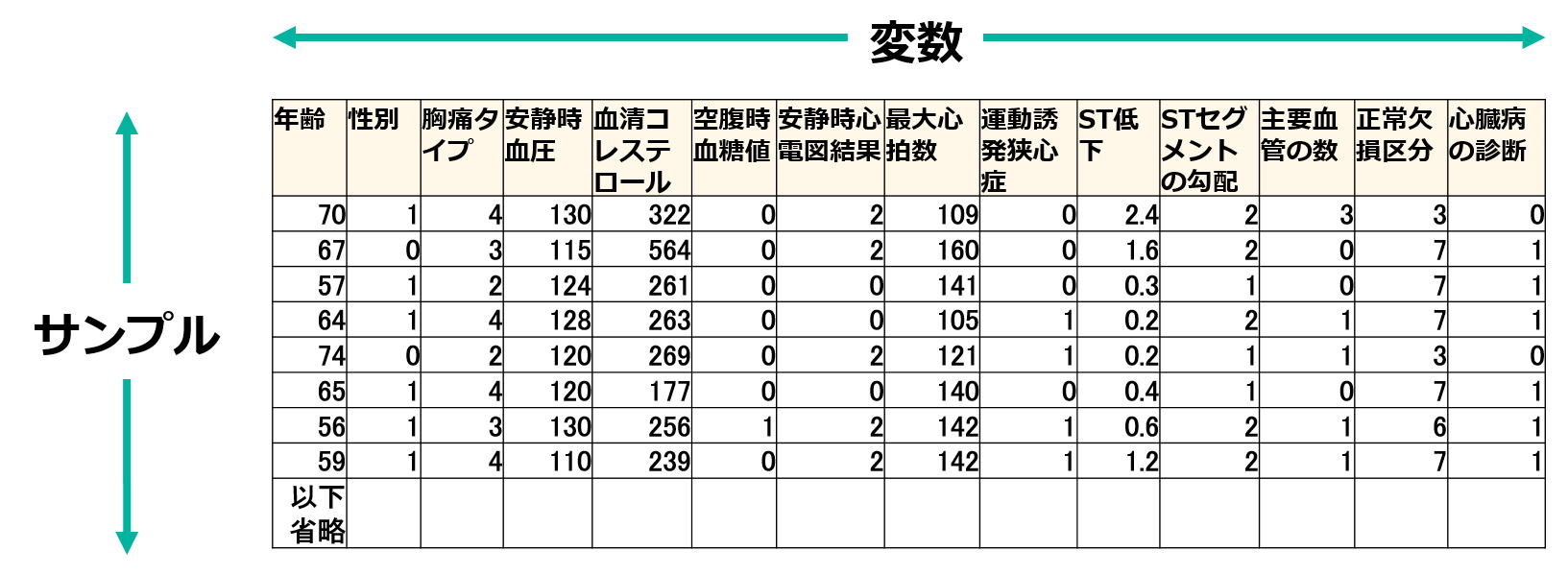
データの内容についてよく理解することはデータ解析を行う上で重要です。各変数の数値がどのような値をとり、どのような意味を持つのか分からないと、分析することができません。

以下のキーワードについて、インターネットなどで調べておきましょう。
　狭心症、コレステロール、T波、ST波

CSV形式のデータは以下のところからダウンロードすることができます。
heart2.csv

UC Irvine Machine Learning Repositoryは、カリフォルニア大学アーバイン校が運営，機械学習やデータマイニングに関するデータを配布しています。

https://archive.ics.uci.edu/ml/datasets/Statlog+%28Heart%29

ここではアルファベットで変数名を定義します。

変数	変数名	説明
年齢	age	年齢（歳）
性別	sex	1 =男性、0 =女性
胸痛タイプ	cp	胸痛タイプ - 1：典型的な狭心症　typical angina - 2：非定型狭心症　atypical angina - 3：非狭心症性の痛み　non-anginal pain - 4：無症状　asymptomatic
安静時血圧	trestbps	入院時mm Hg
血清コレステロール	chol	mg/dl
空腹時血糖値	fbs	空腹時血糖値>120 mg/dl : 1 =真、0 =偽
安静時心電図結果	restecg	- 0：通常　normal - 1：ST-T波異常（T波の反転および/またはSTの上昇または下降>0.05 mV）　　　having ST-T wave abnormality - 2：エステスの基準による左心室肥大の可能性または確定　　　showing probable or definite left ventricular hypertrophy by Estes' criteria
最大心拍数	thalach	拍/分
運動誘発狭心症	exang	1 =はい、0 =いいえ
ST低下	oldpeak	安静時と比較して運動により誘発されたST低下
STセグメントの勾配（ピーク運動）	slope	- 1：上昇 - 2：フラット - 3：下降
主要血管の数	ca	蛍光透視法で着色された、0-3
正常欠損区分	thal	3：正常　normal、6：固定性欠損　fixed defect、7：可逆性欠損　reversable defect
心臓病の診断	heart_disease	0：正常（thal=3） 1：心臓病（thal=6 または 7）

ここでは、正常と心臓病の人（変数：心臓病の診断）がいますが、その人たちの測定値にはどのような違いがあるのかを調べます。心臓病の場合は、6：固定性欠損と、7：可逆性欠損（変数：正常欠損区分）の2種類があります。

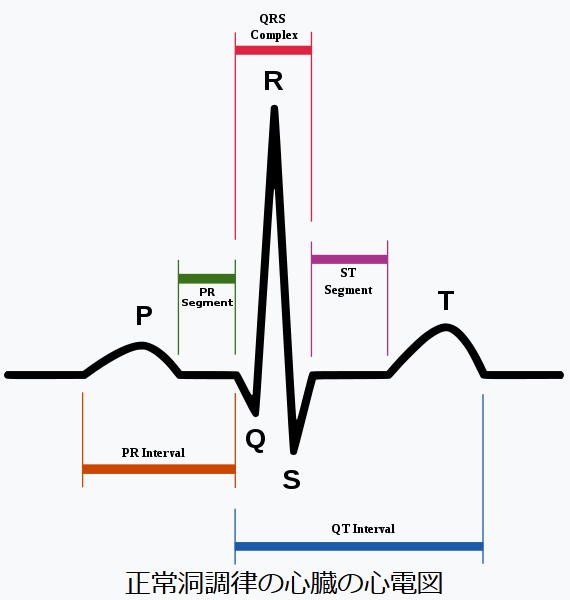
ウィキペディアを参照。

連続量とカテゴリ量について

変数はデータの値の種類により、大きく分けて連続量とカテゴリ量があります。上のデータでは、性別、胸痛タイプ、空腹時血糖値、安静時心電図結果、運動誘発狭心症、正常欠損区分、心臓病の診断がカテゴリ量になります。

データの種類	データの意味	尺度の種類	尺度の意味	データの例
カテゴリ量（質的データ）	分類や種類を区別する。そのままでは足したり引いたり演算はできない。	名義尺度	分類の順序に意味が無く、単なるラベル。	性別、血液型、色
カテゴリ量（質的データ）	分類や種類を区別する。そのままでは足したり引いたり演算はできない。	順序尺度	分類の順序に意味があるもの。	順位、学年、満足度
連続量（量的データ）	数値として意味のあり、足したり引いたり演算ができる。	間隔尺度	データの間隔に意味があるもので、ゼロもひとつの状態にすぎないデータ。	テストの点数、年齢
連続量（量的データ）	数値として意味のあり、足したり引いたり演算ができる。	比例尺度	データの比率に意味があるもので、ゼロが何もないことを意味するデータ。	身長、体重、温度、湿度

ヒストグラムと棒グラフによるデータの確認

ヒストグラムは連続量の変数に対して、棒グラフはカテゴリ量の変数に対して用います。一つの変数の値がどのような分布をしているのか見ることができます。

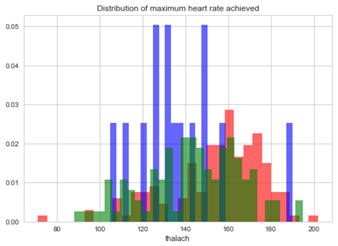
正常（青）と心臓病（赤）の２つのグループを色分けしてヒストグラムを描いています。2つのグループが重なっているところは、赤の色が濃くなっています。グループを分けて描いた場合と比較してください。縦軸は件数ではなく、比率になっています。

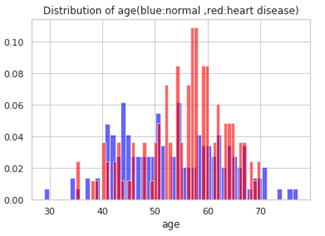
2つのグループを別々のヒストグラムで見てみます。縦軸のスケールが異なることに注意してください。

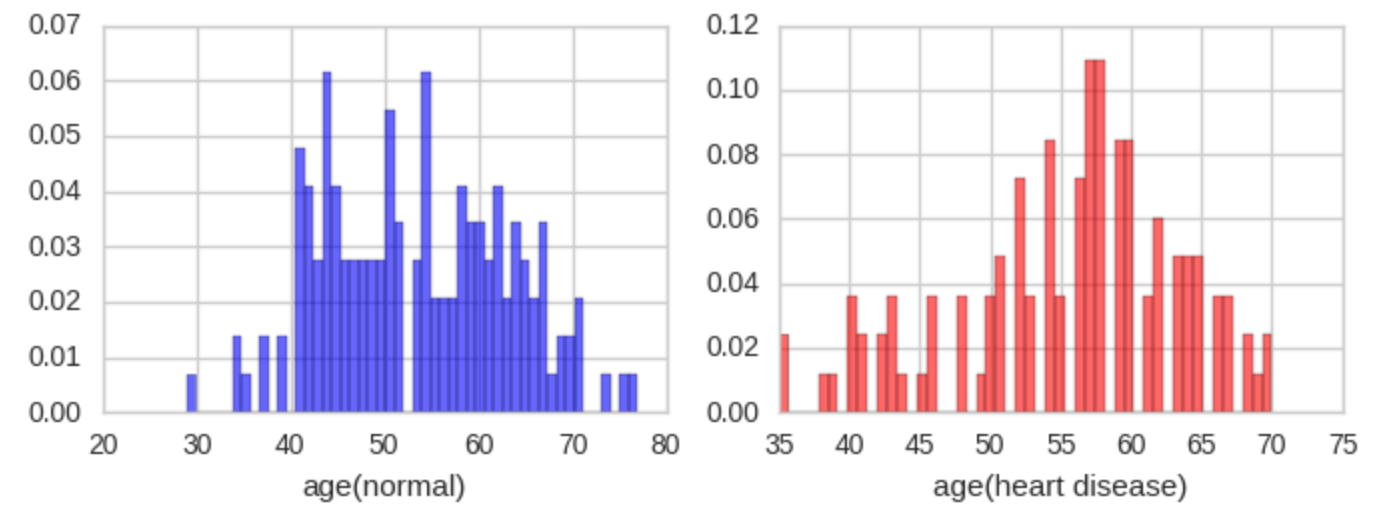
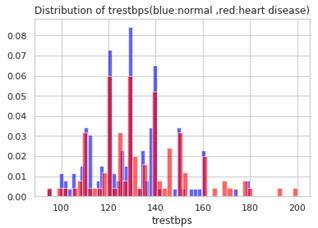
下は安静時血圧です。140より高い人が何人もいますが、赤の心臓病の人が多いようです。

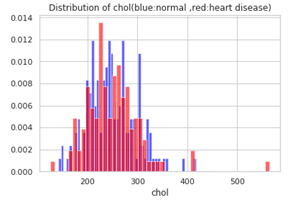
血清コレステロールcholで400を超える人が何人かいます。

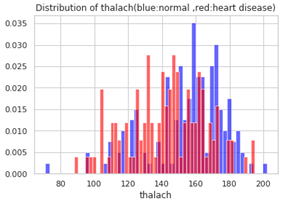
最大心拍数thalachが80以下の人と、200を超える人がいます。

ST低下が心臓病の人に多く見られます。

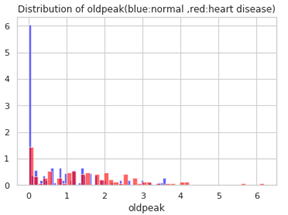
ヒストグラムを見て得られた情報をもとに、以下の点について調べてみましょう。

　血清コレステロールの正常値はどのような範囲でしょうか。
　最大心拍数の正常値はどのような範囲でしょうか。
　ST低下はどのような状況でしょうか。また、心臓病との関係はどうでしょうか。

変数がカテゴリ量の場合は、クロス集計を行い、棒グラフで表示します。クロス集計の正常な人は74人（女性）と78人（男性）、心臓病の人は13人（女性）と105人（男性）となっています。この数値を棒グラフにすると、２つのグラフの上の方になります。

sex 　　　　　　0 　 1
heart_disease
0 　　　　　　74 　78
1 　　　　　　13 105

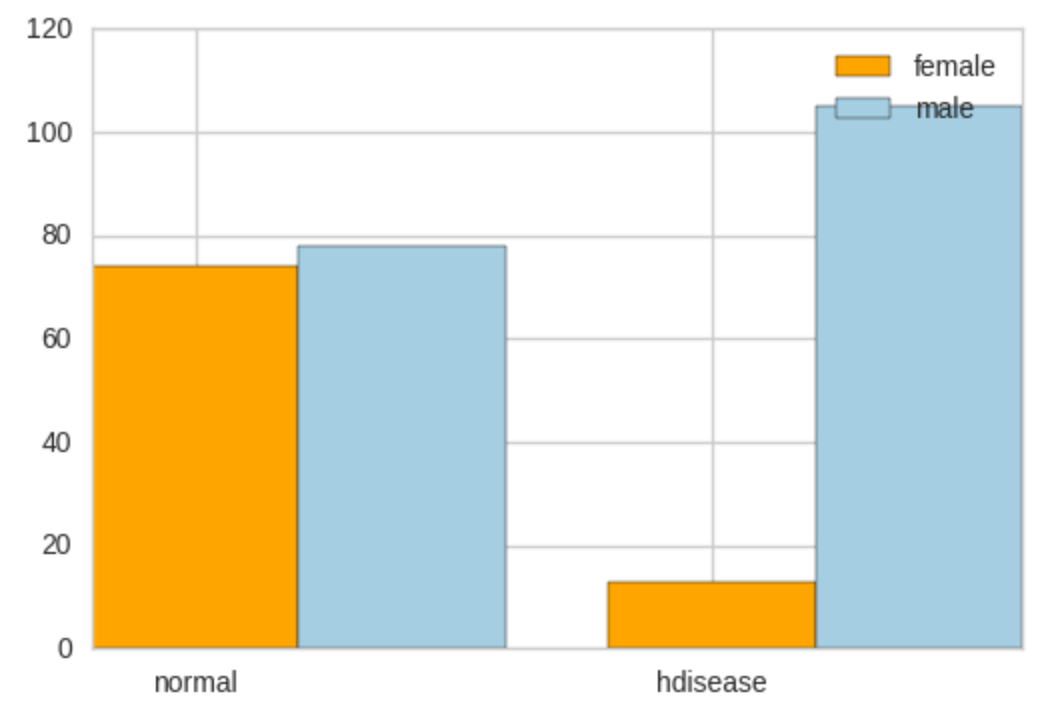
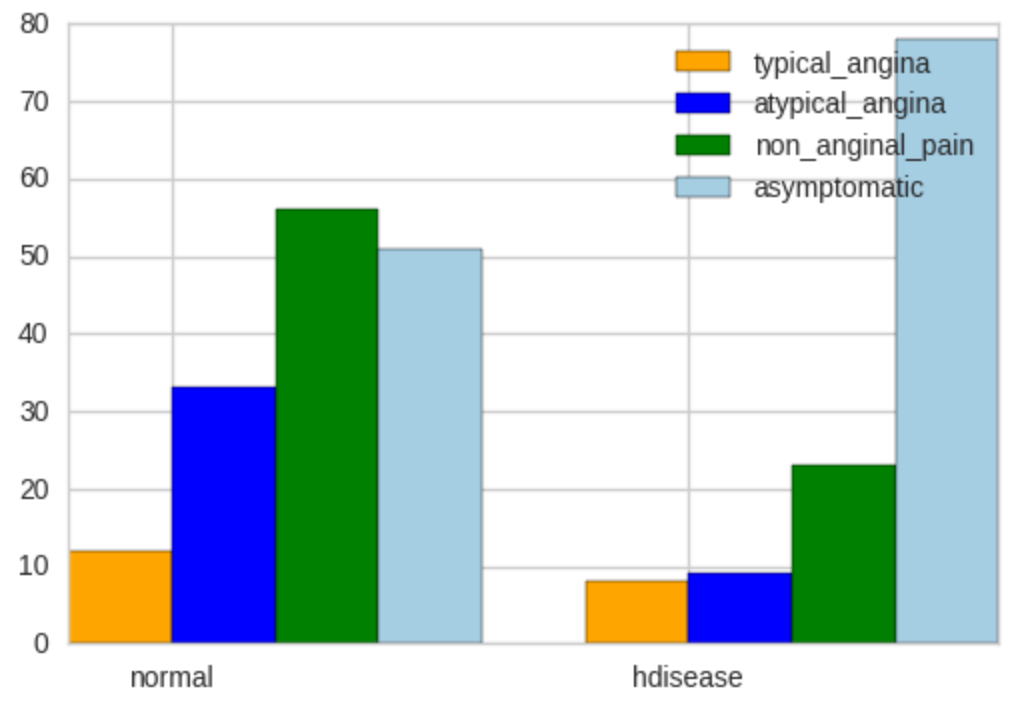
上のグラフで、正常と心臓病の人で、どのような違いがあるのかを考えてみましょう。

平均値と標準偏差

平均値や標準偏差などの基礎統計量を見ます。上が正常で、下が心臓病の人です。

trestbps（安静時血圧）の平均値は、正常と心臓病でそれぞれ、129.223684と134.076271ですが、これが統計的に有意な差なのか調べてみます。

仮説検定について

2つのグループのtrestbps（安静時血圧）の平均値には差があるかどうか、仮説検定にもとづくと、この評価には以下の２つの仮説がたてられます。

帰無仮説H0　：　μ1=μ2
対立仮説H1　：　μ1≠μ2

検定の手順：
1.母集団からデータ（標本）をランダムに取り出し、命題に対する検定統計量t値を、取り出したデータから計算します。
2.帰無仮説H0とこれを否定する対立仮説H1は上記のとおりです。
3.有意水準（棄却域）αを決めます。（5%、1%など）
4.検定統計量はt分布にしたがうので、p値と棄却域（有意水準）αとの関係は以下のようになります。

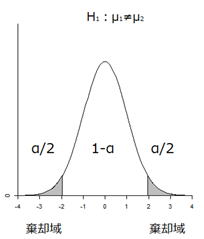
検定統計量が棄却域に入る場合p<α（下図の右側）、H0が生じる確率は十分に小さいと判断してH0を棄却して、H1を採択します。?

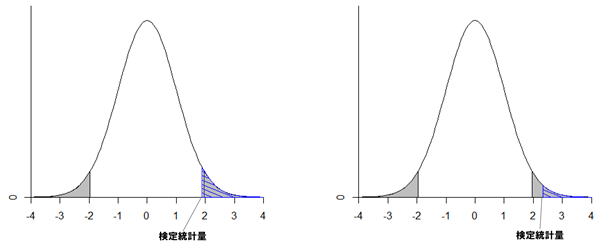
5. p>αならば（上図の左側）、H0を棄却しません。

上の確率（p値）が非常に小さい場合，ほとんど起きない事象が起きたことになります。しかしこれは，稀な事象が起きたと考えるより，仮説が間違っていたと考える方が自然です。つまり仮説は棄却され，対立仮説が採択されることになります。

参考文献：橋本洋志、データサイエンス教本、オーム社
石村貞夫、すぐわかる統計解析、東京図書

平均値の差の検定

２つのグループの平均値に差があるかどうかみてみます。有意水準を5%としておきます。
平均値の差の検定を行いますが、2群の分散が等しいかどうかで、検定の方式が異なります。そのために、等分散性の検定を行います。まず仮説は以下のようになります。

　帰無仮説H0　：　2つの分散は等しい。
　対立仮説H1　：　2つの分散は等しくない。

各グループのサンプル数( n1, n2)や不偏分散から検定統計量F0（分散比）を求めます。検定統計量は、自由度が( n1-1, n2-1)のF分布にしたがいます。

等分散性の検定の結果はつぎのようになります。検定統計量F0（分散比）は3.2573 ｐ値は0.0711であり、5%の有意水準では有意になりません。つまり、等分散であるということです。

平均値の差の検定では、帰無仮説は以下のようになります。
　帰無仮説H0　：　2つの平均値には差がない。
　対立仮説H1　：　2つの平均値には差がある

検定統計量t値は、等分散のときとそうでないときでは式が少し異なりますが、t値と自由度を求めることにより、平均値の差の検定ができます。

等分散の場合の平均値の差の検定は以下のとおりです。有意水準を5%とした場合、0.0265は5%より小さいので、帰無仮説は棄却されます。つまり、平均値に差があるということです。
　検定統計量 t値=2.2305, p値=0.0265

PythonやRで表示される統計量などの値は、2.2305881807606882など桁数が多い数字です。しかし、複雑な統計計算をしていることと、PythonやRの数値の精度が15～16桁程度ですので、このように多くの桁数の数値を示すことは意味がありません。4～5桁程度が意味のある精度ですので、ここでは、4～5桁程度で表示をします。

分散分析と多重比較

正常欠損区分thal（3：正常、6：固定性欠損、7：可逆性欠損）ごとの最大心拍数thalachの分布を見てみます。

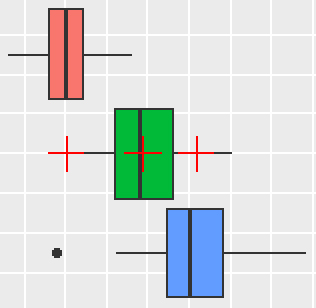
ボックスプロットや平均値の比較をしてみます。３つのグループには違いがありそうです。
　　Thal
　　3 　155.019737
　　6 　136.571429
　　7 　143.634615

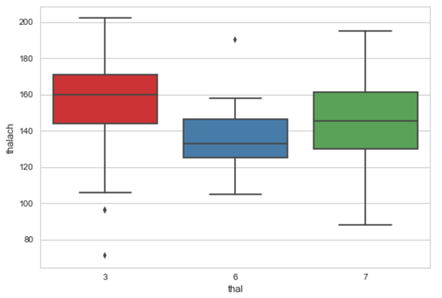
3グループ間には差があるように見えますが、統計的に有意な差であるかどうか1元配置分散分析でしらべてみます。1元配置分散分析では、3つ以上のグループがあるとき、それらのグループ間に差があるかどうか調べます。
　帰無仮説H0：μ1=μ2＝μ3=…
1元配置分散分析の分散分析表は以下のとおりです。p値は0.00004と非常に小さく、5%の有意水準と比べても小さいので、帰無仮説は棄却されます。

チューキーのHSD (honestly significant difference) 検定

チューキーの範囲検定、チューキー法としても知られています。この方法は、互いに有意に差がある平均を探索するために分散分析と併用されます。チューキー法では全ての可能な平均の対を比較し、「スチューデント化された範囲分布」(q) を用います（この分布はt検定に用いられるt分布に似ています）。

Multiple Comparison of Means - Tukey HSD,FWER=0.05

下の結果についてはつぎのとおりです。

3と6、3と７については、平均値の差がー10以上あり、その95%信頼区間もマイナスですので、帰無仮説は棄却されます。3と6、3と７については有意な差が認められるということです。
6と7については、平均値の差が7.0632であり、その95%信頼区間に0が入っており、棄却はされませんでした。つまり、6と7については有意な差はないということです。


テキストファイル入力		ヒストグラムと棒グラフ		平均値と標準偏差		平均値の差の検定		分散分析と多重比較

正常	age	trestbps	chol	thalach	oldpeak
count	152	152	152	152	152
mean	53.539474	129.223684	248.868421	155.019737	0.728289
std	9.805987	16.45753	48.553471	22.239357	0.936205
min	29	94	141	71	0
max	77	180	417	202	3.6

心臓病	age	trestbps	chol	thalach	oldpeak
count	118	118	118	118	118
mean	55.584746	134.076271	250.677966	142.79661	1.464407
std	8.01849	19.250555	55.657205	22.598525	1.255588
min	35	94	126	88	0
max	70	200	564	195	6.2

	df	sum_sq	mean_sq	F	PR(>F)
C(thal)	2	10540.48192	5270.240961	10.515396	0.00004
Residual	267	133818.4847	501.192827

group1	group2	meandiff	lower	upper	reject
3	6	-18.4483	-33.186	-3.7106	TRUE
3	7	-11.3851	-18.1001	-4.6702	TRUE
6	7	7.0632	-7.9586	22.085	FALSE