データ解析・機械学習解析事例集

時系列解析、統計解析、データ解析や機械学習に関する実データにもとづいた解析事例集です。RやPythonなどのスクリプト（部分）はこのページの最後にリンクがあります。

分析する上で重要なことは、データについてよく理解することです。さらに、グラフや分析結果で何か特徴が見つかったら、それがその分野の知識と照らし合わせて、問題がないかどうか検討することが必要です。

解析の流れは以下のようになります。


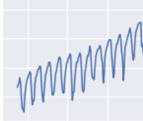
テキストファイル入力		折れ線グラフ		トレンドと季節変動による予測		ARIMA モデルの推定		SARIMA モデルの推定

時系列解析について

時系列データ：時間とともに変動し、時間（秒、分、時、月．．．）に依存した系列を時系列データといいます。四半期ごとの物価の変動、日々の外国為替の変動、月ごとの太陽黒点の推移などがあります。

この時系列データにもとづく分析を時系列解析あるいは時系列分析といいます。

大気中のCO2濃度の解析：時間の経過による濃度の変化について調べて、将来の予測をします。

まず、データについてよく理解します。

このデータは、岩手県の綾里にある観測所で測定された、大気中のCO2濃度です。1987年1月から月ごとのデータです。

CSV形式のデータは以下のところからダウンロードすることができます。
co2.csv

単位 ppm ： ppmは大気中の分子100万個中にある対象物質の個数を表す単位です。

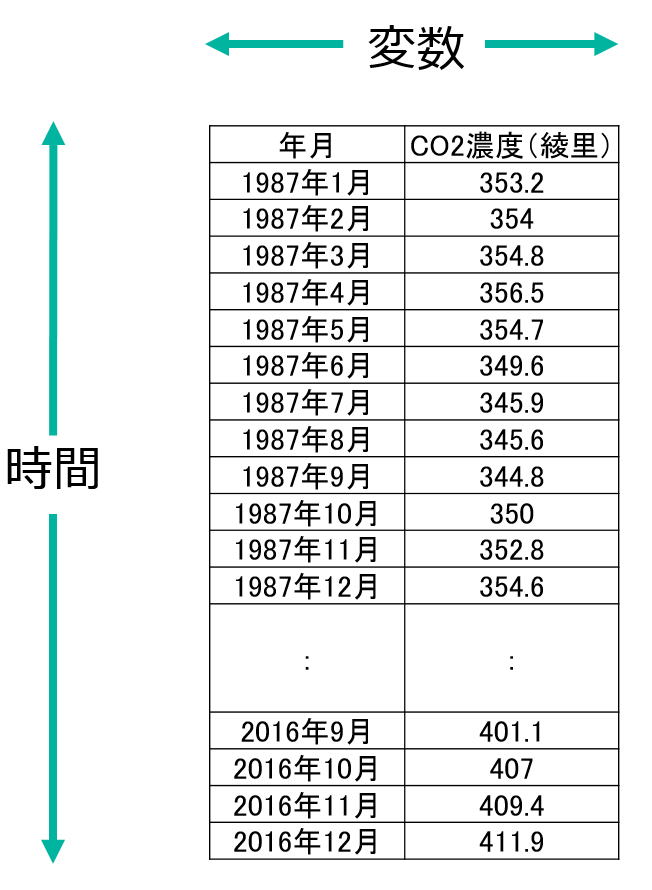
気象庁のHPより

https://ds.data.jma.go.jp/ghg/kanshi/obs/co2_monthave_ryo.html

綾里の気象庁の観測所は、下の地図に示すように、岩手県の大船渡市の近くにあります。

折れ線グラフによるデータの確認

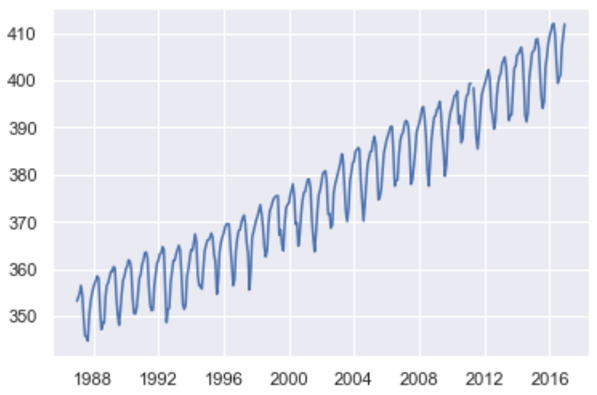
扱うデータは、1987年1月から2016年12月までの月ごとのデータです。2017年1月以降は速報値なので、2016年までのものを用います。

分析の対象は1987年1月から2010年12月として、2011年1月以降は予測の検証用とします。

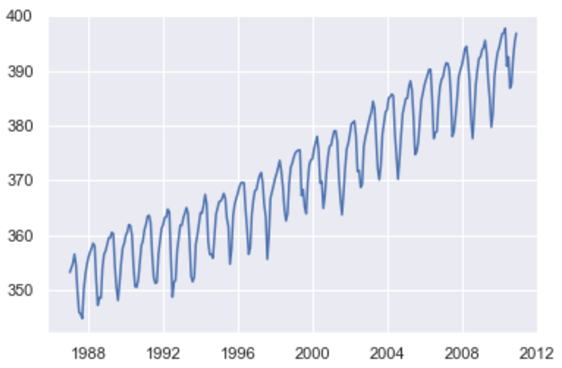
CO2の変動について
グラフを見ると、年ごとに増加しており、季節による変動があることが分かります。これについては以下のように、気象庁のHPに説明があります。
■濃度の変化を見ると、2つの大きな特徴があります。
　1年間の平均値を比較すると、濃度は年々増加している
　1年の内で周期的な季節変動をする
■増加の原因には、人間活動に伴う化石燃料の消費、セメント生産、森林破壊などの土地利用の変化などが挙げられます。
■工業化以前の時代からの増加の6割以上が、化石燃料の消費やセメント生産によるものです。残りの増加は、農法の変化による寄与を含めて、森林破壊を主とした土地利用変化（と関連するバイオマス燃焼）によるものです。排出された二酸化炭素の一部は植物や海洋によって吸収されていますが、残りは大気中に蓄積されます。
■二酸化炭素濃度の季節変動は、植物の光合成による二酸化炭素の吸収と、植物等の呼吸や分解による二酸化炭素の放出が、それぞれ異なる季節変動をするために起きるものです。

大気中のCO2濃度の予測：２つの方法

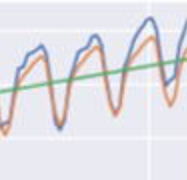
トレンドと季節変動による予測：
時系列データを、傾向変動あるいはトレンド（長期にわたる一定方向の変化）と周期的な季節変動、循環変動、不規則変動などの要因に分けることにより、予測をします。時系列＝傾向変動+循環変動＋季節変動+不規則変動

SARIMAモデルによる予測：
時系列データの各時点間のデータの並び順や前後関係に関係性がある場合、自己回帰モデル（AR）や移動平均モデル（MA）、あるいはこれらの合成のモデルを仮定することにより、予測をすることができます。

トレンドと季節変動による予測

時系列データを以下の要因に分けることにより予測を行います。
　時系列＝傾向変動+循環変動＋季節変動+不規則変動

移動平均によるトレンドの抽出

中心化移動平均は、両端の期の重みを半分にした加重平均を用いて、第 k 期の 12 項移動平均は次のように定義されます。

トレンド、季節変動、不規則変動の分離

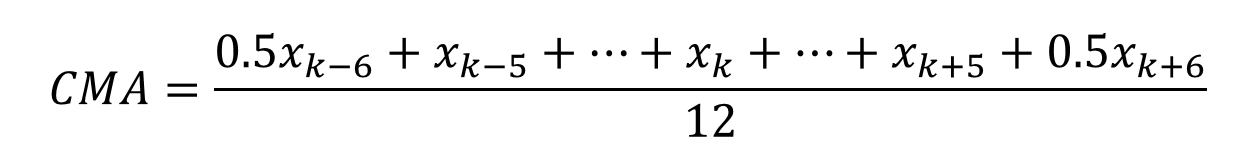
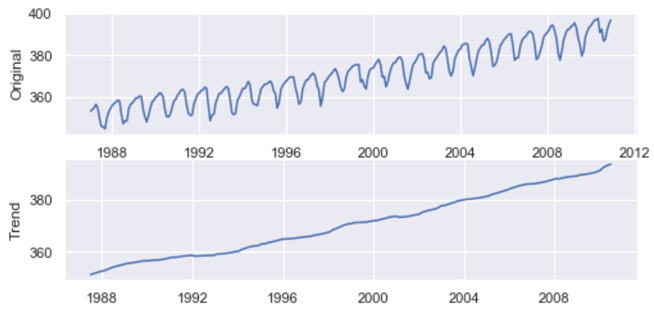
Pythonのtsa.seasonal.seasonal_decompose関数によりトレンド（傾向変動）、季節変動、不規則変動を分離することができます。それぞれの最初の12か月分の値を表示しています。既定値の場合、このデータでは、12項中心化移動平均法により、トレンドを抽出します。

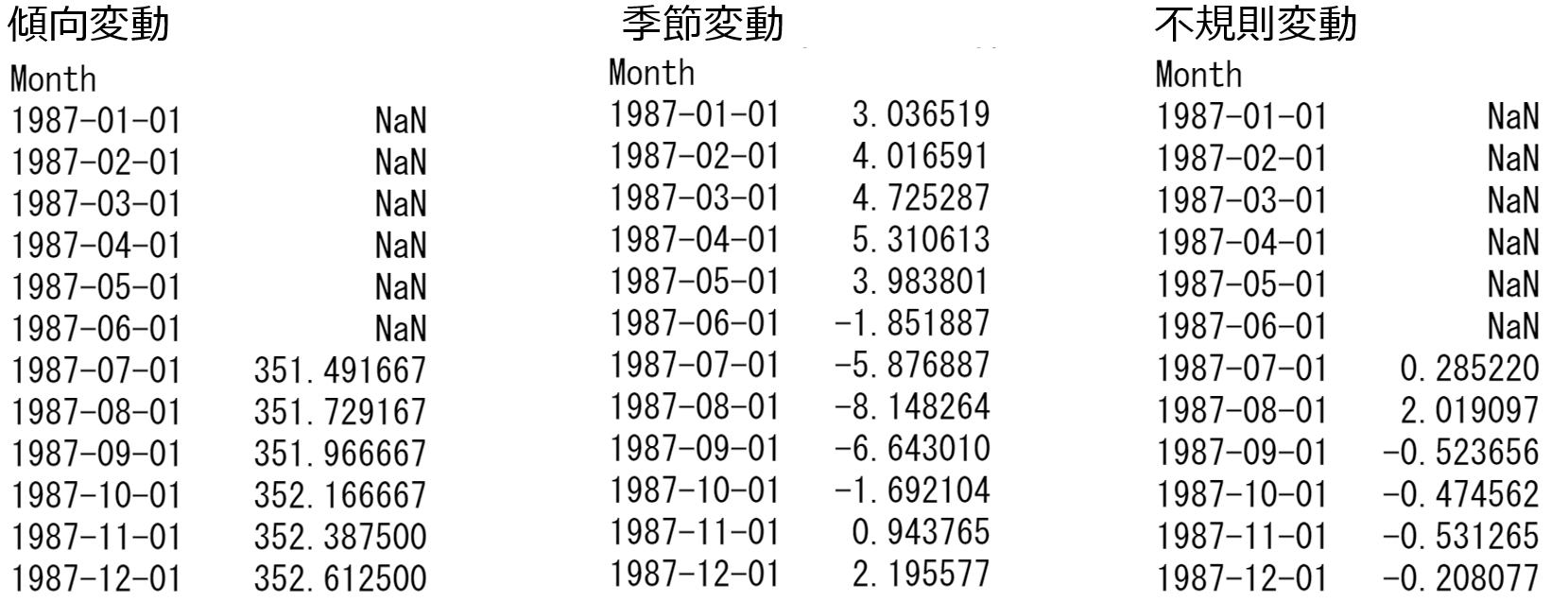
以下のグラフはそれぞれ原系列、トレンド、季節変動、不規則変動です。

トレンドへの回帰モデルのあてはめ

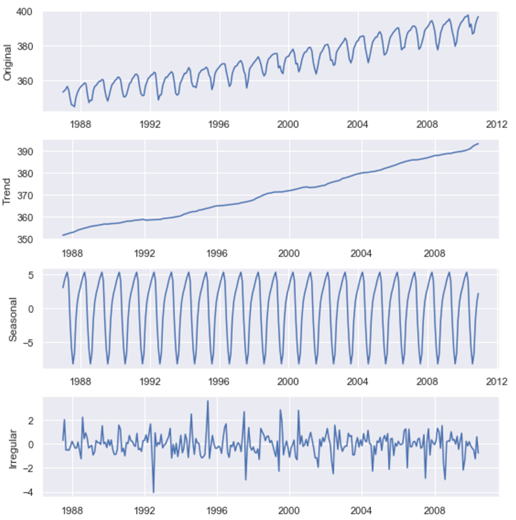
上で抽出したトレンドに回帰モデルにあてはめて、トレンドを予測します。この場合、トレンドはほぼ直線なので、１次回帰式にあてはめます。また、x軸は1、２、３、…のように月ごとの時点を１きざみの値にしています。トレンドは、最初と最後の6か月は欠測値のため、７から２８３までをｘの値としています。

回帰分析の説明変数ｘの値をここでは、1987年1月を1、 1987年2月を2．．．とおいています。

傾向変動は1987年7月から2010年6月なので、xは7から283の値を取ります。

結果は、以下のようになりました。
　　y=349.5602+0.1472*x1

抽出された季節変動

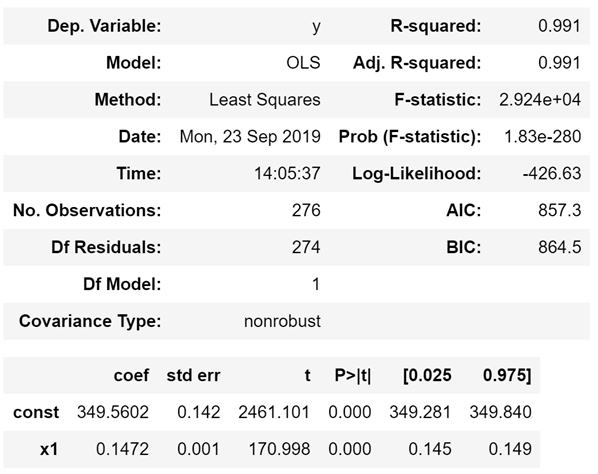
抽出された季節変動は、以下のように１年分は同じ値です。したがって、トレンドの予測値の各年には同じ季節変動を加えることにより、全体の予測ができます。

２０１６年までのトレンド予測

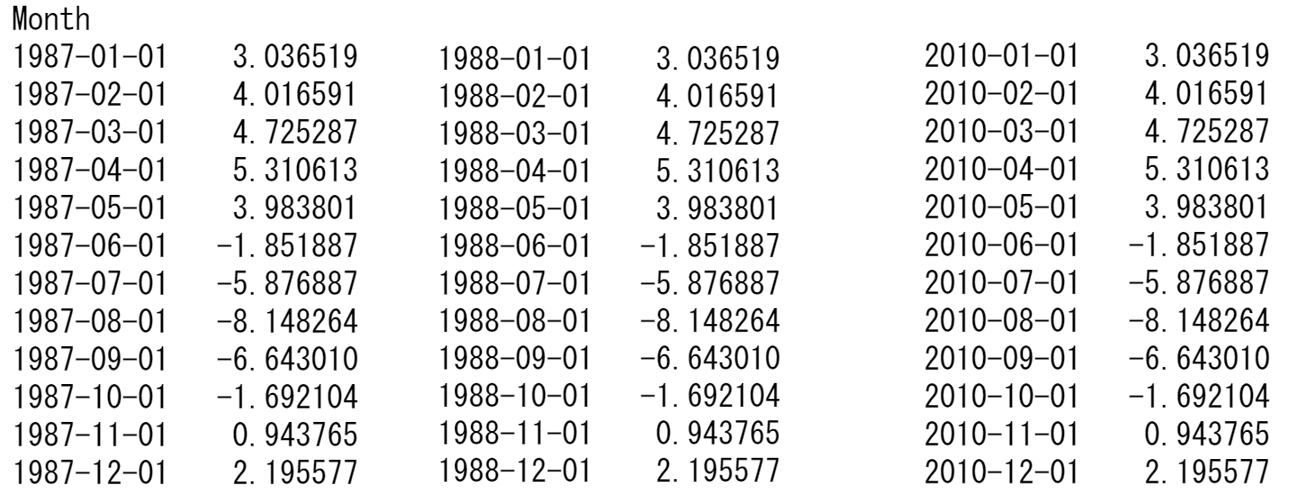
①推定された回帰式にあてはめて、トレンドを予測します。
②トレンドに季節変動を重ねます。
③年月のデータを生成します。
④年月、原系列、トレンド、予測値を1つのデータフレームにします。

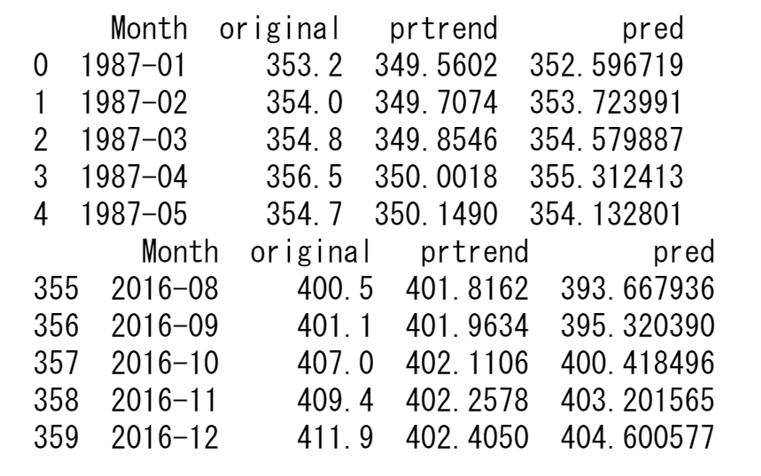
原系列とトレンドの予測値、全体の予測値をプロットすると以下のようになります。

ARIMAモデルによる予測

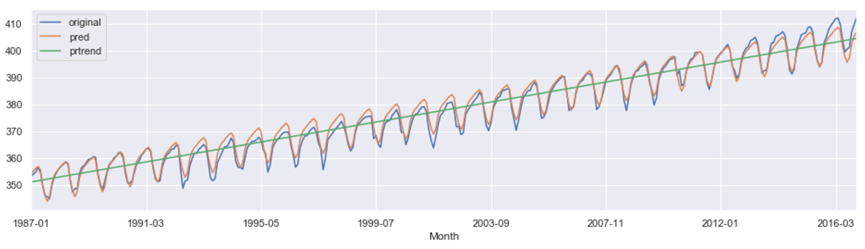
時系列データは確率過程からの標本

時系列分析では、データが「確率過程」という確率的なしくみに従い、時間軸にそって次々に出現してくるものと考えます。すなわち、ある時点t+1に変数yt+1がどのような値をどのような確率でとるかなどが、すべて時点tについて1つの規則として定められたものが確率過程です。

確率過程では、時点ｰ∞から時点+∞までの確率変数の集まりで、われわれが観測するデータ（たとえば、1987年1月から2016年12月までの綾里におけるCO2濃度）は、それらが全体で確率過程の一部分として出現した1つの標本であると考えます。

時系列分析では、確率過程について数学モデルをつくり、これにデータをあてはめて、様々な判断や予測などを行います。　

参考：田中孝文：Rによる時系列分析入門、シーエーピー出版

自己相関係数

２つの変数XとYとの関係を示すものとして相関係数がありますが、1つの時系列データに対して、すべての異なる時点間に相関係数が定義され、それを自己相関係数と呼びます。

自己相関係数（ACF:Autocorrelation Function）は、過去の値が現在のデータにどれくらい影響しているか、その関係性を見ます。

ずらしたデータのステップ数をラグ（lag)とよびます。

ACFはykとyt−kとの間の線形的な相関の強さを示しています。

下図は自己相関係数のグラフです。ACFは、ラグが12、24、36で高くなっており、12の周期をもっていることが分かります。

偏自己相関係数

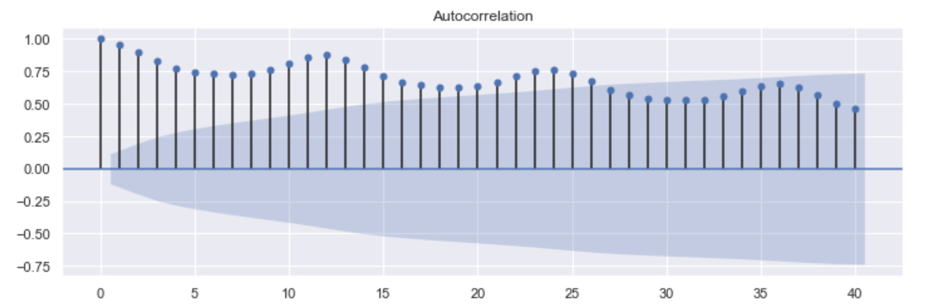
偏自己相関係数（PACF:Partial Autocorrelation Function）は自己相関係数から、時間によって受ける影響を除去した自己相関係数です。

今月と2か月前の関係には間接的に1か月前の影響が含まれます。偏自己相関係数を使うと、1か月前の影響を除いて今月と2か月前だけの関係を見ることができます。

PCAFはykとyt−kに対するyt−k以外の項(yt−k+1など)の影響を除いた相関の強さを示しています。

下図は偏自己相関係数のグラフです。

ARIMAモデルの推定

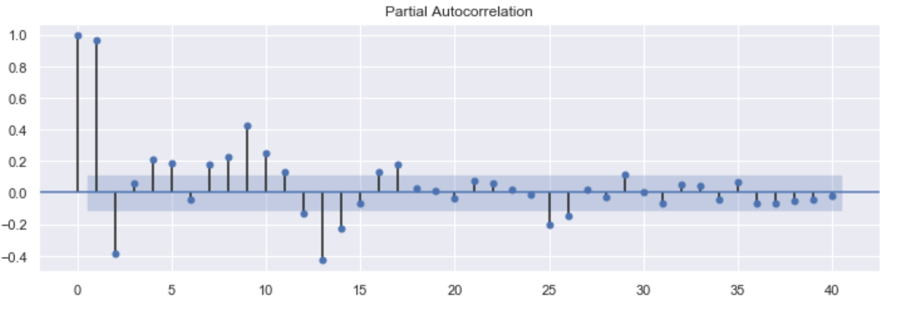
■ARIMA過程（自己回帰和分移動平均過程）
d階差分を取った系列が定常かつ反転可能なARMA(p,q)過程に従う過程は次数(p,d,q)のARIMA(p,d,q)過程と呼ばれます。

■d階差分
系列をy1,y2,y3,…,ynとすると、1階差分を取った系列は、 Δyk=yk-yk-1 (1≦k≦n)で構成されます。2階差分は1階差分の系列から同様の差分を取った系列で、以下同様にd階差分も同様です。

■AR過程（自己回帰過程）
AR過程（自己回帰過程）は、ある時刻のデータが、過去の時刻のデータから表現することができる過程です。p次のAR過程であるAR(p)は、以下のように表される過程です。cは定数、εtは誤差項で平均0、標準偏差σの正規分布に従います。
yt=c+ψ1yt-1+ψ2yt-2+...+ψpyt-p+εt

■MA過程（移動平均過程）
ある時刻のデータが、過去の時刻での誤差項を用いて表現することができる過程で、q次のMA過程MA(q)は、以下のように表されます。
yt=c+θ1εt-1+θ2εt-2+...+θpεt-p+εt
AR過程、MA過程ともに、注目しているデータと過去のデータとの関係を表す方法です。

■ARMA過程(自己回帰移動平均過程)
AR過程とMA過程を組み合わせて表現される過程です。ARMA(p, q)は、以下のように表されます。
yt=c+ψ1yt-1+ψ2yt-2+...+ψpyt-p+θ1εt-1+θ2εt-2+...+θpεt-p+εt

■定常過程
任意のtとkに対して、以下が成立する場合，過程は定常過程といわれます。
E(yt)=μ
Cov(yt,yt-k)=E[(yt-μ)(yt-k-μ)]=γk
V(yt)=σ²

参考：沖本竜義：経済・ファイナンスデータの計量時系列分析、朝倉書店

1階差分を取った系列に対して、自動ARMA推定関数により、次数(p,q)を推定します。

p=4, q=2 と求まったので、ARIMA(4,1,2)のモデルを推定します。ar.L1.D.co2_ayasotはψ1、ma.L1.D.co2.ayasatoはθ1に対応します。

SARIMAモデルの推定

ARIMAモデルの拡張として、季節成分を取り入れたものをSARIMAモデルと呼びます。

CO2濃度の月単位のデータで説明します。通常のARIMAモデルでは、データを月ごとにとり、「先月の濃度が高ければ今月も高い」と、前後の月の関係からモデルを構築します。一方で、SARIMAモデルでは、データを前年同月で取り、「去年の４月が高かったので、今年の1月も高い」といったように、過去の同月との相関関係をモデル化します。

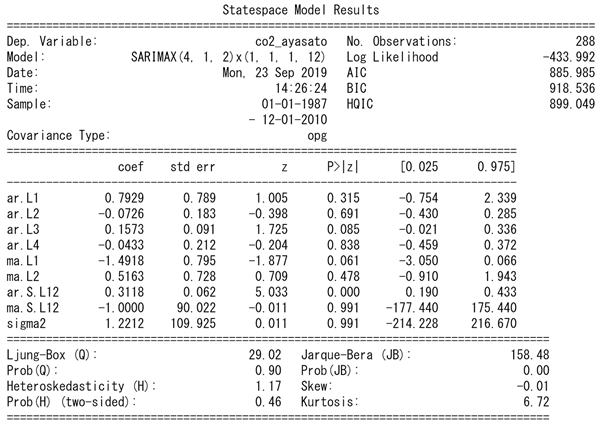
自己相関係数と偏自己相関係数を見てみます。

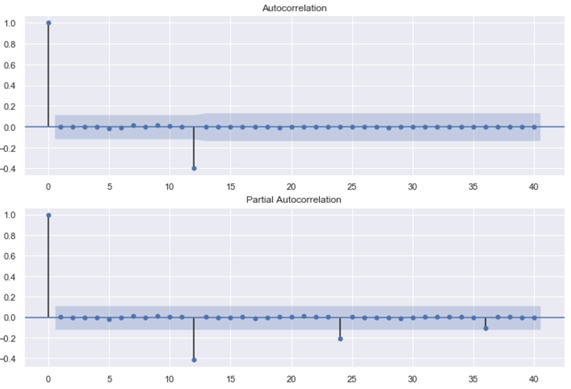
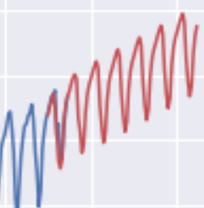
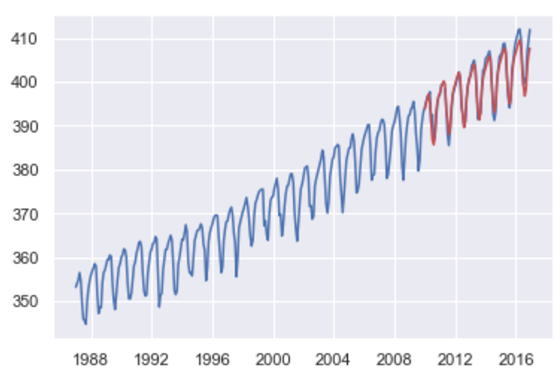
求まったSARIMAモデルによって2016年まで予測することができます。

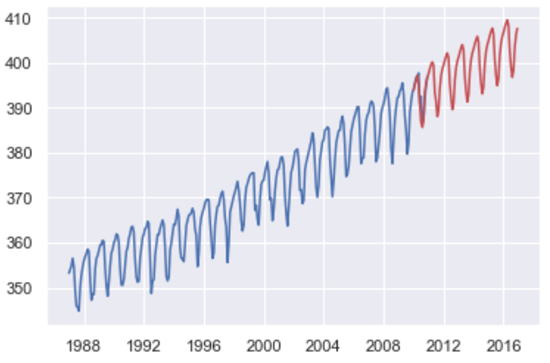
2011年から2016年までの予測値と実データをプロットして比較してみます。

Pythonによるスクリプト

co2_01_python.py
スクリプトと結果は一部分です。全体はセミナーのときに紹介します。