
アワビデータの解析

アワビデータの解析
統計解析、データ解析や機械学習に関する実データにもとづいた解析事例集です。RやPythonなどのスクリプトと結果(部分)はこのページの最後にリンクがあります。
解析する上で重要なことは、データについてよく理解することです。さらに、グラフや分析結果で何か特徴が見つかったら、それがその分野の知識と照らし合わせて、問題がないかどうか検討することが必要です。

解析の流れは以下のようになります。
 |
|
 |
 |
 |
||||||
| テキストファイル入力 | ヒストグラム や散布図 |
主成分分析 による分類 |
回帰分析 | 決定木 による予測 |
ランダム フォレスト |
まず、データについてよく理解します。
データの内容についてよく理解することはデータ解析を行う上で重要です。各変数の数値がどのような値をとり、どのような意味を持つのか分からないと、分析することができません。
CSV形式のデータは以下のところからダウンロードすることができます。
abalone.csv
UC Irvine Machine Learning Repositoryは、カリフォルニア大学アーバイン校が運営,機械学習やデータマイニングに関するデータを配布しています。
https://archive.ics.uci.edu/ml/datasets/Abalone

ここではアルファベットで変数名を定義します。物理的測定からアワビの年齢を予測します。アワビの年齢は殻を円錐形に切り、それを染色し、顕微鏡を使ってリングの数を数えます。より入手しやすい他の測定値は年齢を予測するために使用されます。
| 変数 | 変数名 | 説明 |
| 性別 | Sex | M、F、I(幼貝) |
| 殻の長さ | Length | 殻の最も長いところ(mm) |
| 直径 | Diam | (mm) |
| 高さ | Height | 殻付きの肉の高さ(mm) |
| 重さ | Whole | すべての重量(g) |
| 肉の部分の重さ | Shucked | (g) |
| 腸重量 | Viscera | 血液を除いた腸重量 |
| 殻の重さ | Shell | 乾燥後の殻の重さ |
| リング | Rings | +1.5にすると年齢になります(年) |
データの件数は4177です。最初の5件を表示します。ここでは、リングRingsを連続量として、他の変数から予測する問題を考えます。
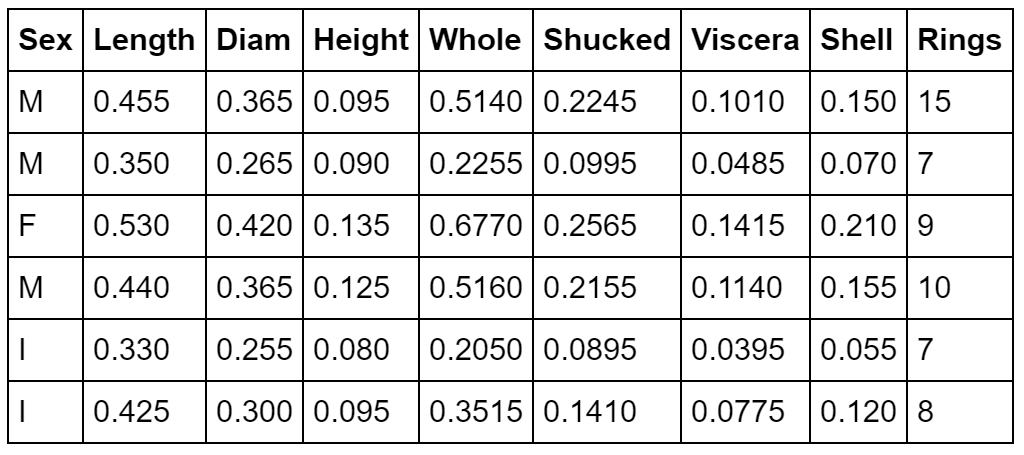
各変数の平均値や分散などは以下のとおりです。
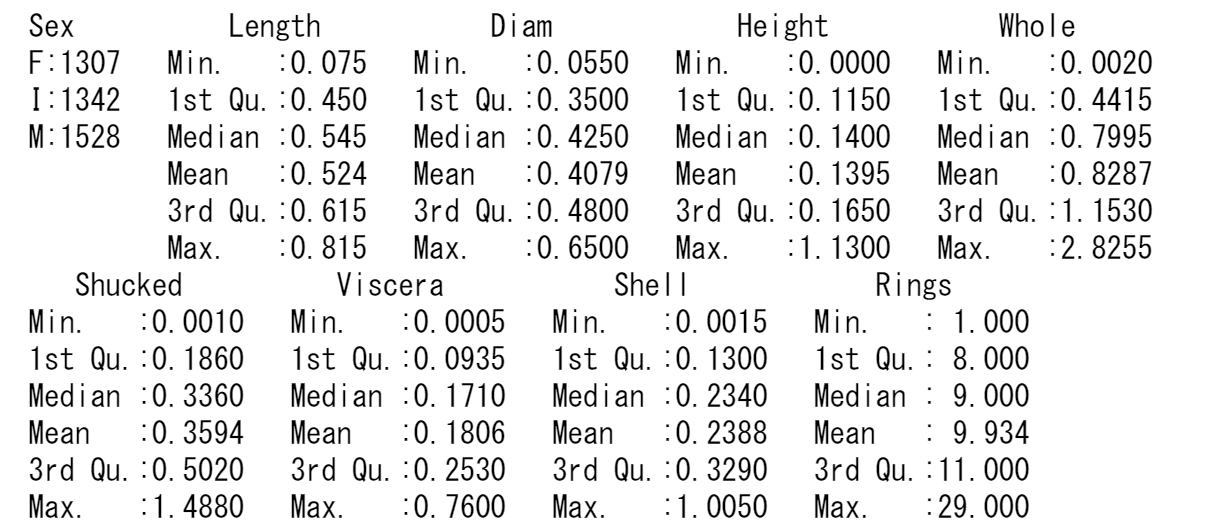
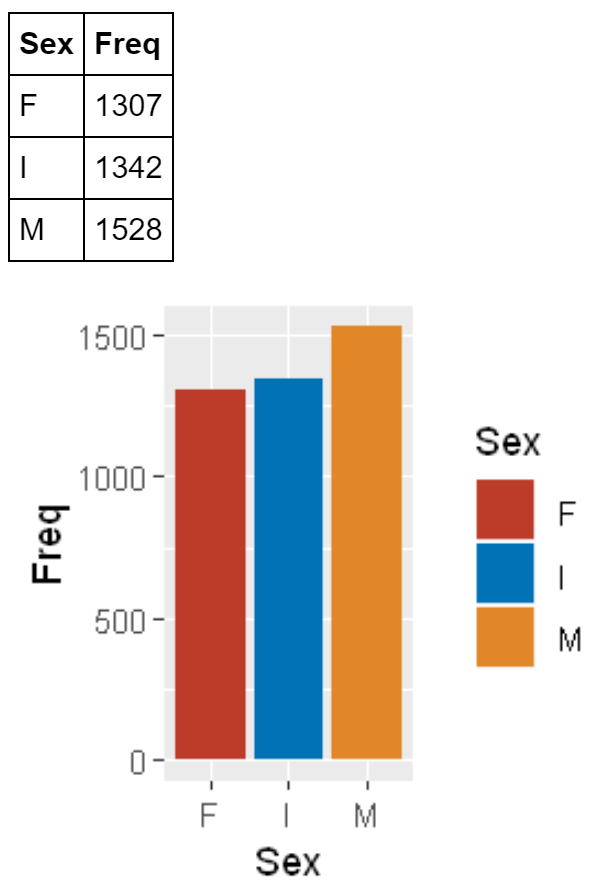
ヒストグラムは連続量の変数に対して、棒グラフはカテゴリ量の変数に対して用います。一つの変数の値がどのような分布をしているのか見ることができます。
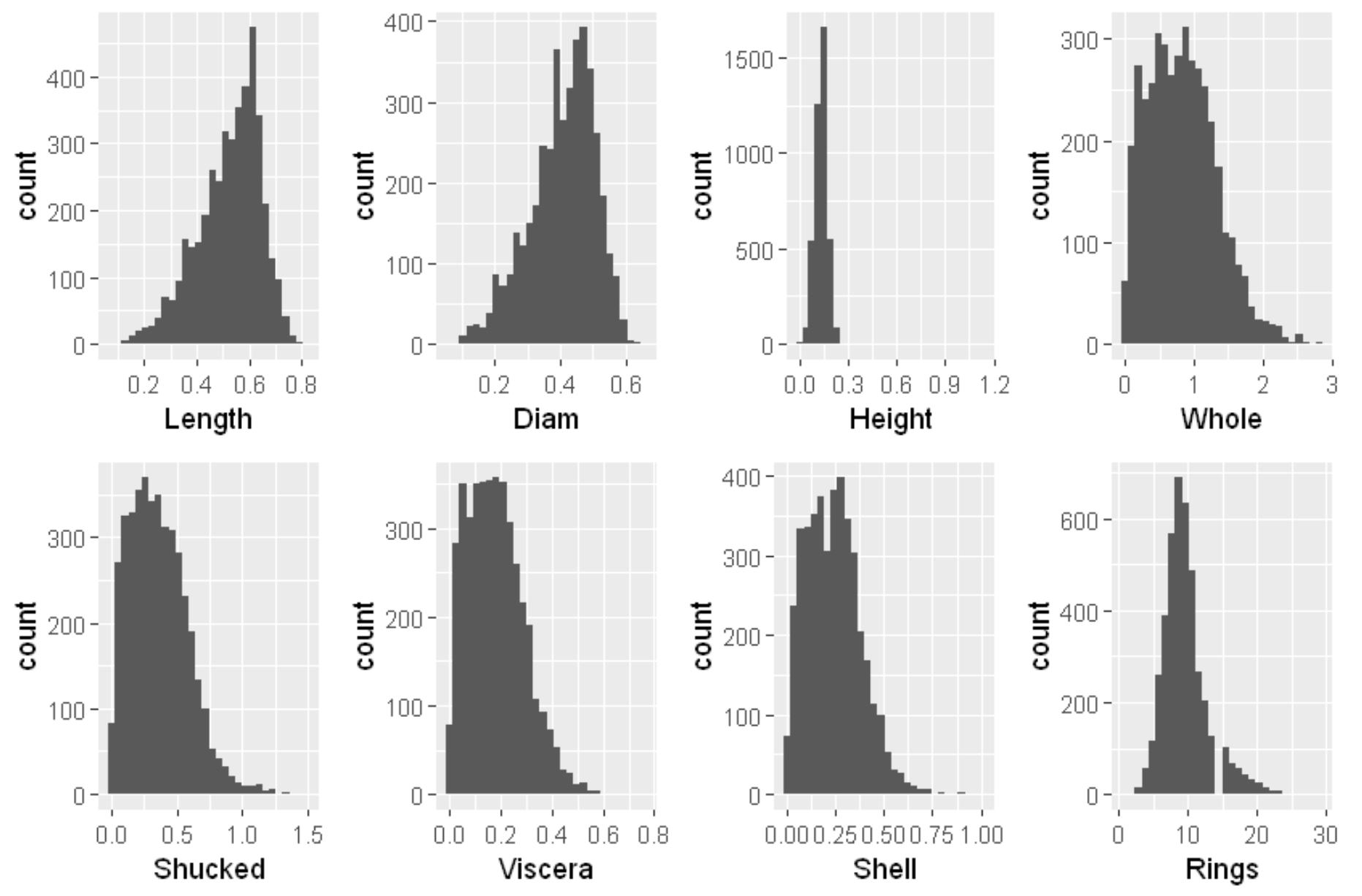
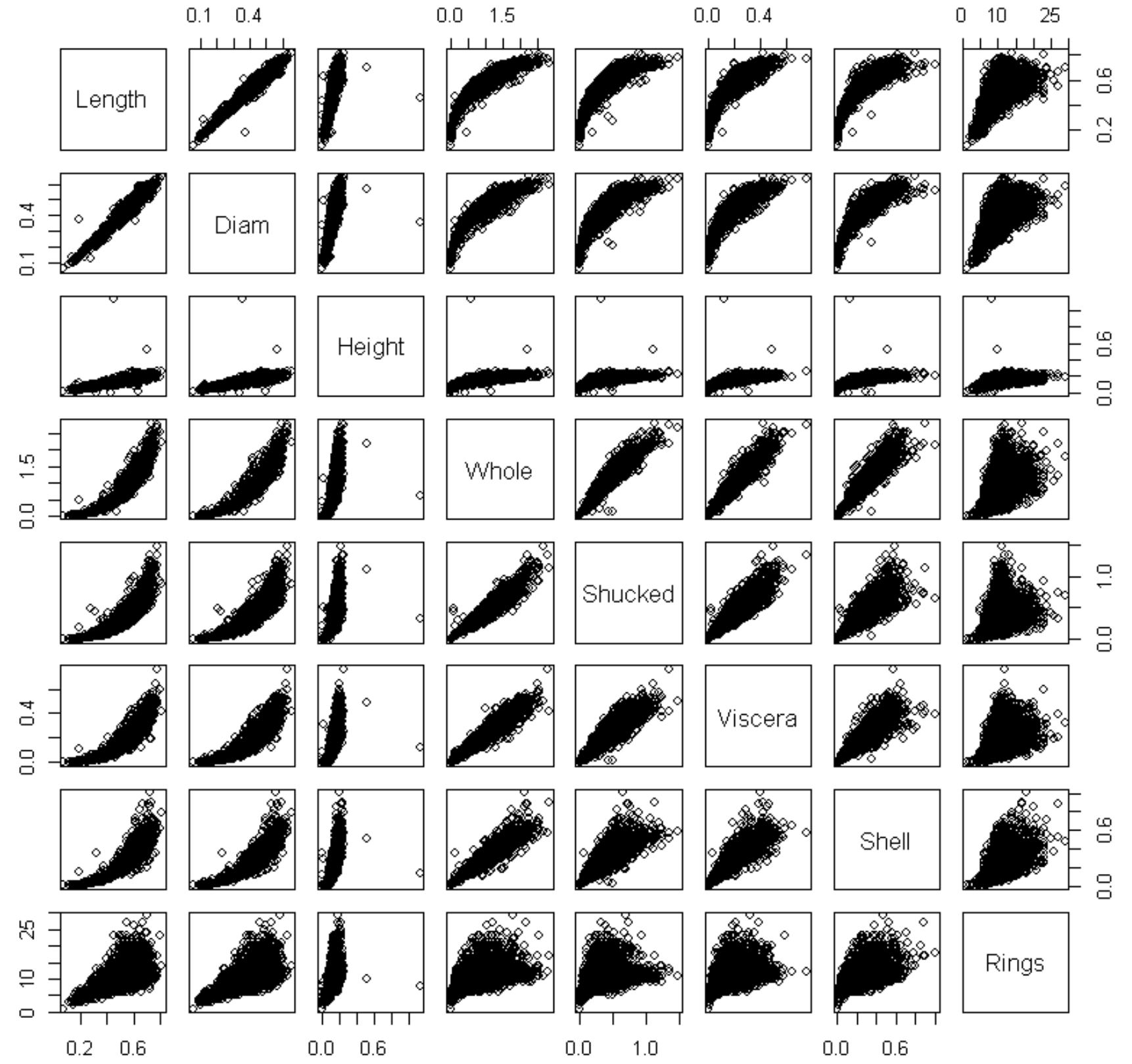
連続変数の散布図行列は以下のようになります。
相関係数を見てみます。
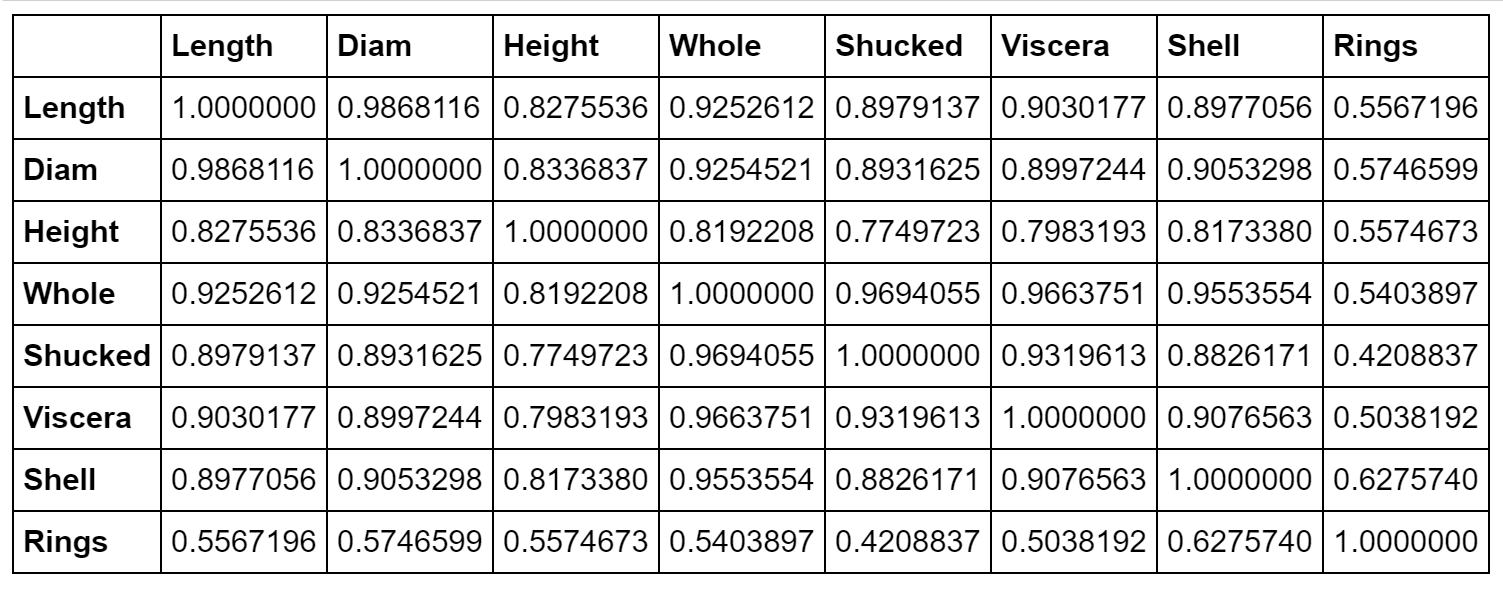
Heightには数個の他よりも大きな値があるため、0.5よりも大きなデータを除いておきます。そうすると、散布図は以下のようになります。Heightと他の変数との関係が見やすくなりました。
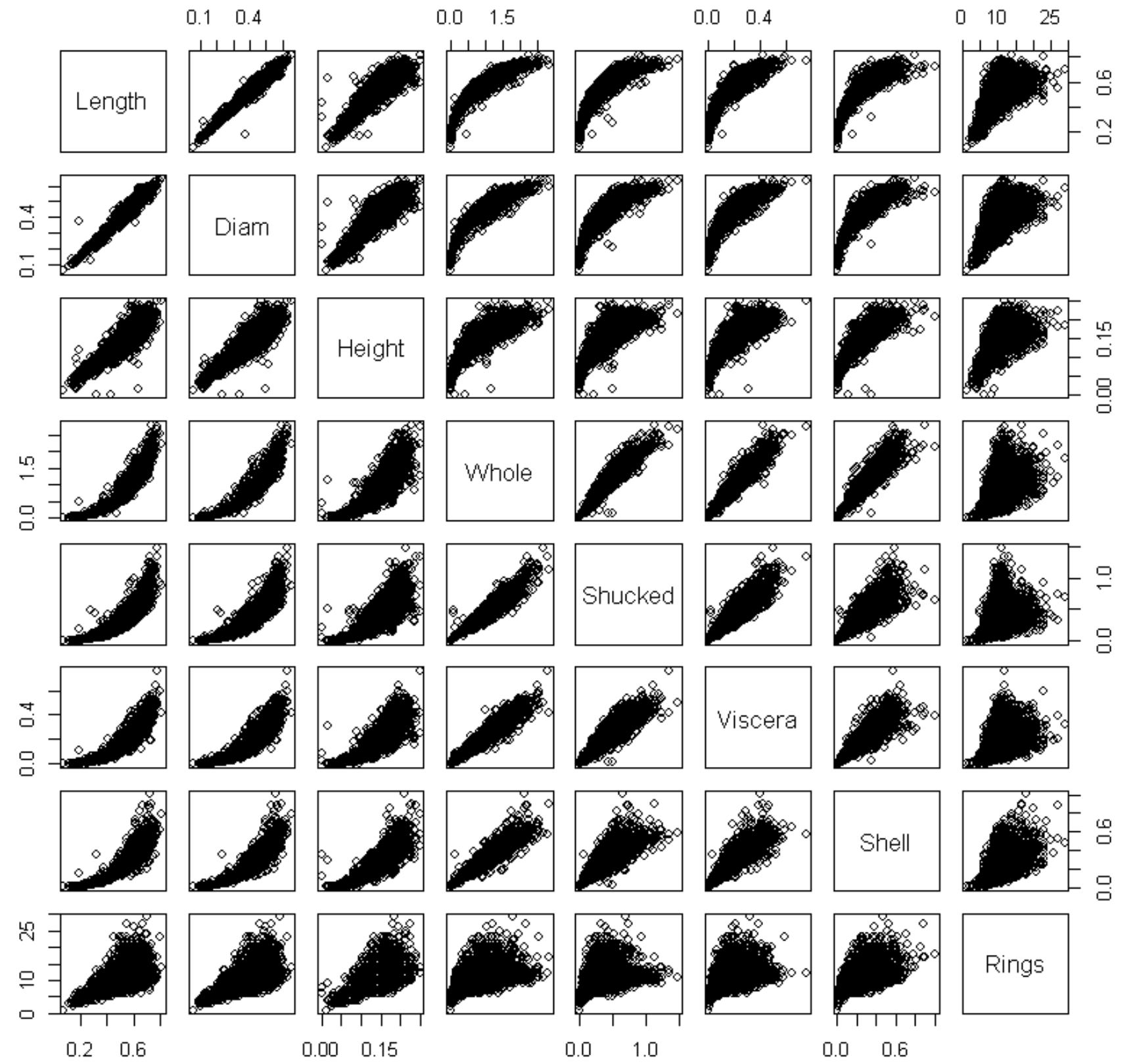
主成分分析とは、多くの変数の値を、1個または少数個の総合的指標(主成分)に代表させようという手法です。これにより、多くの変数を持つデータを、少ない次元で表すことができ、変数や観測値の分類なども可能になります。
変数x1,x2,...xp に対して任意の係数(ak1,ak2,...,akp),k=1,2,..m,m≦pを用いて、以下のようなp変数の一次結合を作ります。x1,x2,...xp は連続量の変数です。
z1=a11x1+a12x2+...+a1pXp
z2=a21x1+a22x2+...+a2pXp
:
zm=am1x1+am2x2+...+ampXp
係数aを次の条件を満足するように定めます。
条件1:(ak1)2+(ak2)2+...+(akp)2=1
条件2:第1主成分の係数a11,a12,...,a1pは、z1の分散が最大になるように定めます。
条件3:第k主成分の係数ak1,ak2,...,akpは、
zkが、z1,...,zk-1と無相関になるように定めます。
上の条件を満たすように係数aを求めるには、相関係数行列または分散共分散行列から固有値・固有ベクトルを計算することになります。一般的には、変数の単位の違いをなくすために相関係数行列から計算します。求まった固有ベクトルが係数aになります。各z1、z2、...が、それぞれ第1主成分、第2主成分、...となります。
固有値の大きさにより、各主成分の情報量が分かります。相関係数行列から計算した場合、p個の固有値の合計はpになるので、固有値をpで割ることにより寄与率が計算されます。
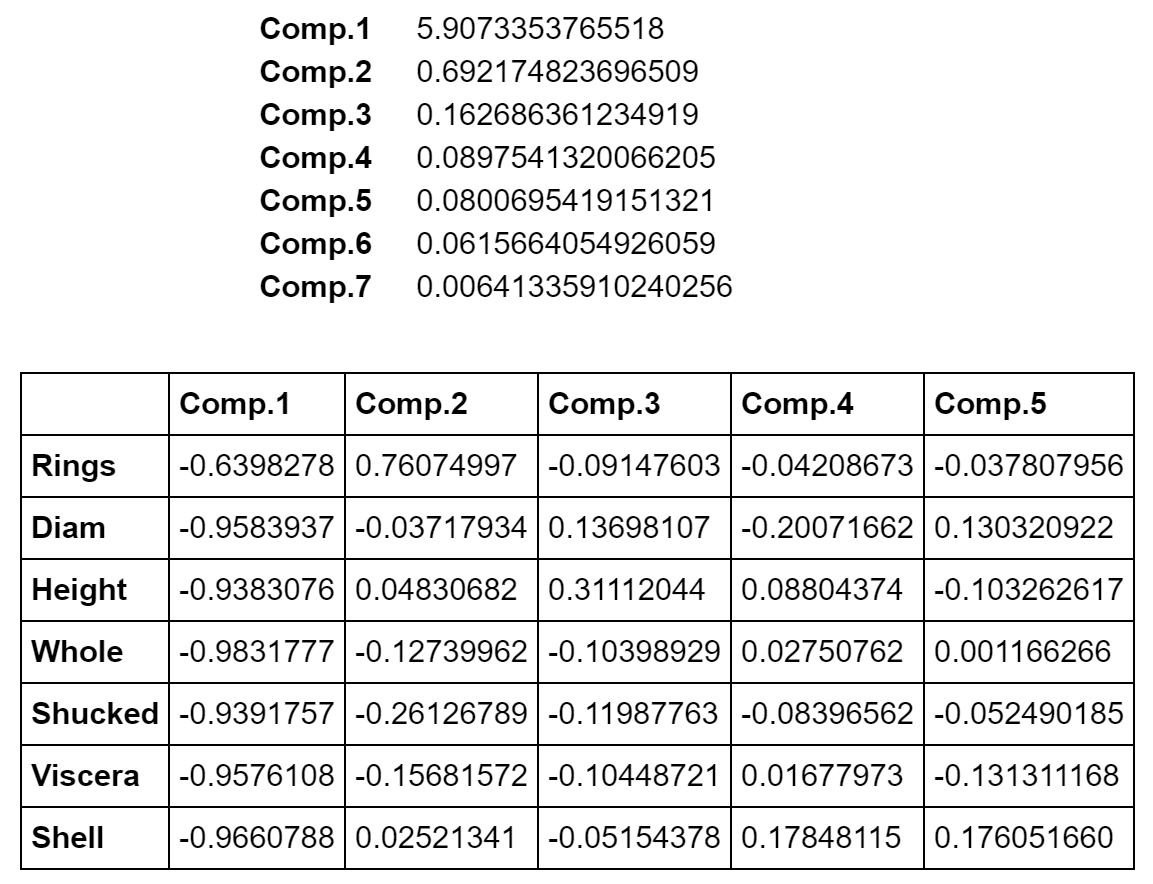
まず、固有値と固有ベクトルを見ます。第1主成分の寄与率は0.843、第2主成分の寄与率は0.099となり、2つの主成分で全体の情報量の94.2%の情報量があります。
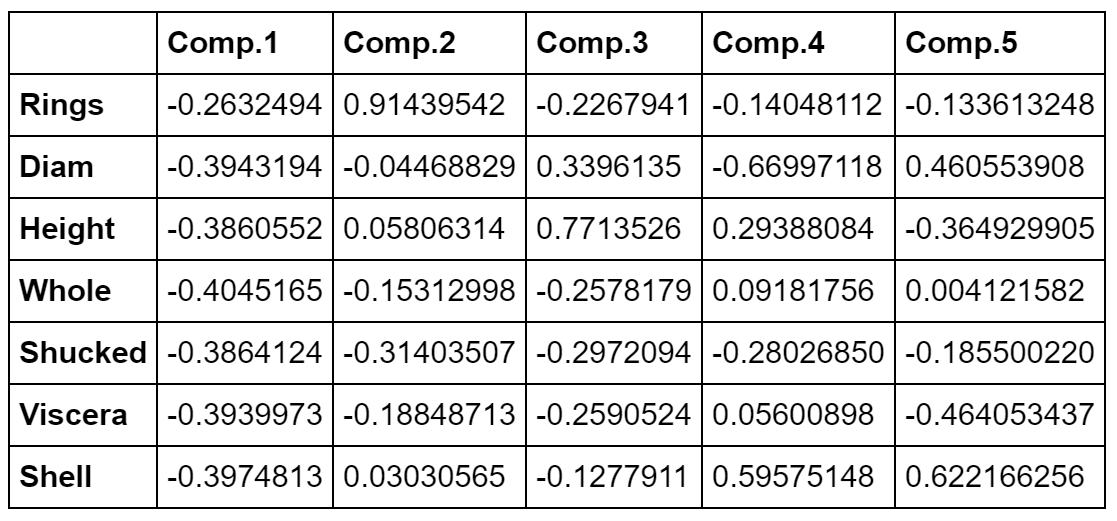
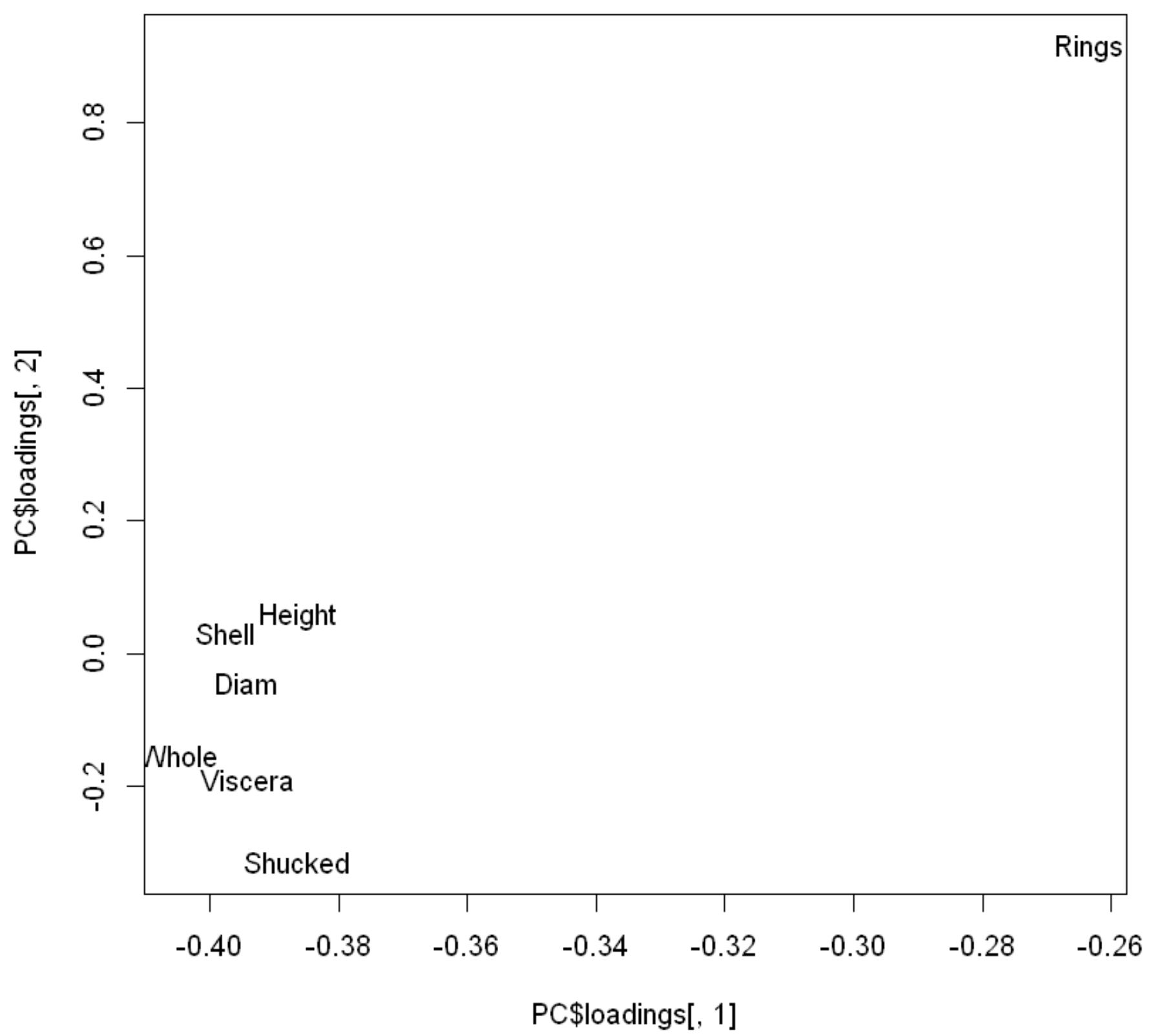
下は主成分負荷量とそのプロット図です。主成分負荷量は、変数と各主成分との相関係数です。プロット図を見ることにより、変数間の関係が分かります。Ringが離れたところにあり、Ring以外の変数がかたまっています。相関係数を見ると、Ringと他の変数との相関はそれほど高くありませんが、Ring以外の変数間の相関係数は0.8以上あり関係が強いことが分かります。これが、主成分負荷量のプロット図に表れています。
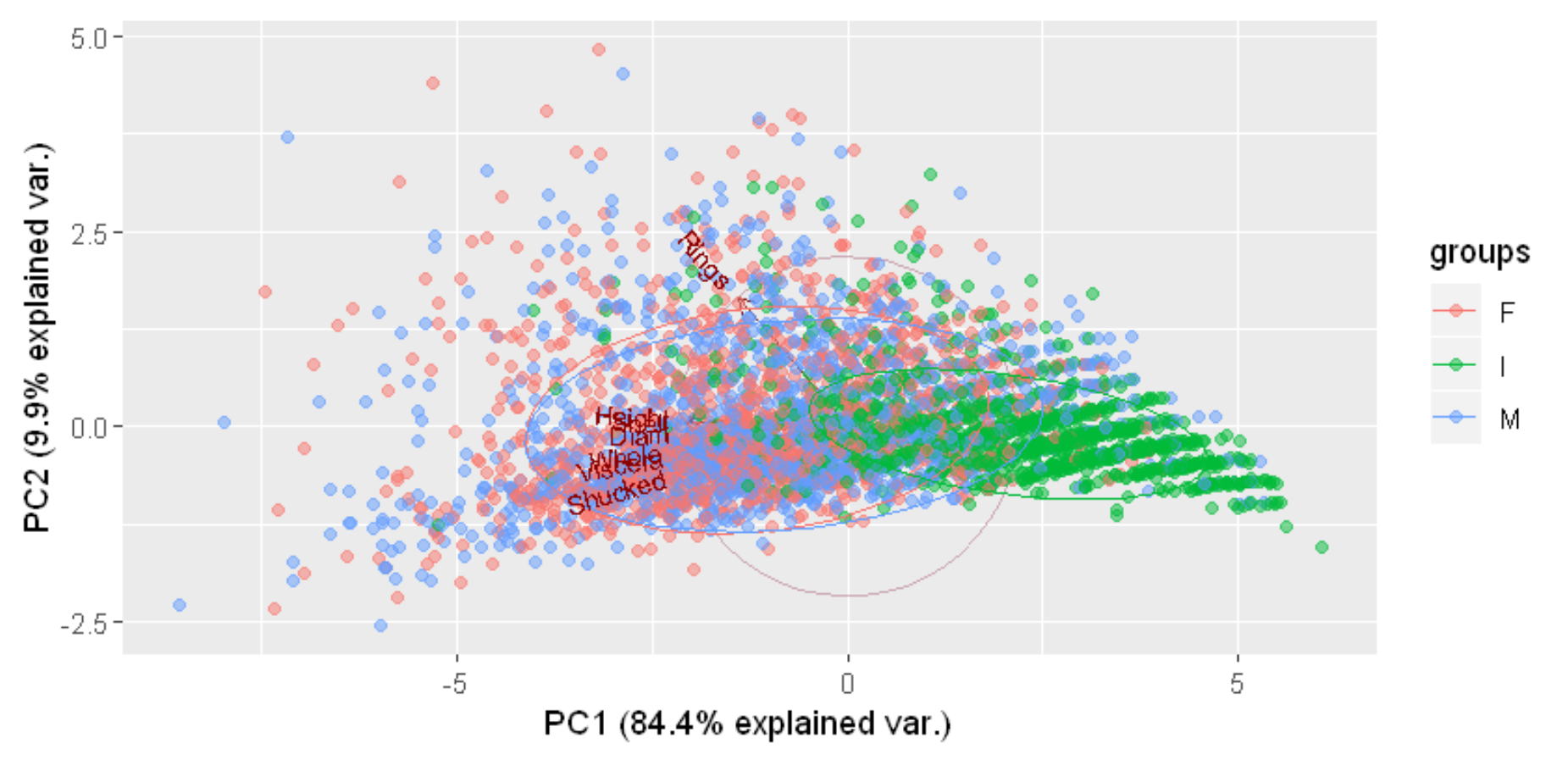
バイプロットにより、変数間の関係、変数と観測値との関係を見ることができます。第1主成分(X軸)は大きさを表しています。幼貝(緑)は大きさや重さも小さいため右の方にあり、MとFは大きくなっているため左の方にあります。第2主成分はRingに関係しており、年齢の軸と言えそうですが、寄与率が9.9%と低い値です。
回帰分析は、説明変数の情報を利用して目的変数の値を予測する手法です。
目的変数:回帰式を使って予測する変数で、従属変数ともよばれます。
説明変数:目的変数を予測する際に使用する変数で、独立変数ともよばれます。 一般に、目的変数の値を予測するための式として、目的変数の一次式(線型式)が用いられます。
y=a0+a1x1+a2x2+...+apxp
この式を回帰式とよび、a0,a1,a2,….,apをデータから推定するパラメータで、a0を定数項、a1,a2,….,apを回帰係数といいます。各パラメータは、最小2乗法により推定されます。具体的には、観測値と予測値との差(残差)の2乗和を最小にするようにパラメータの値を決めます。下のデータによる回帰モデルは以下のように表されます。左辺が目的変数、右辺が説明変数です。
Ring=a0+a1Sex+a2Diam+a3Height+...+a7Shell
参考文献:山口和範、よくわかる統計解析の基本と仕組み、秀和システム
まず、性別Sexはカテゴリ量であるため、ダミー変数に変換します。Rの場合は、Sexをfactor関数で因子化することにより、説明変数として用いることができます。Sexは3つのカテゴリがありますが、1つ目は除いてあります。
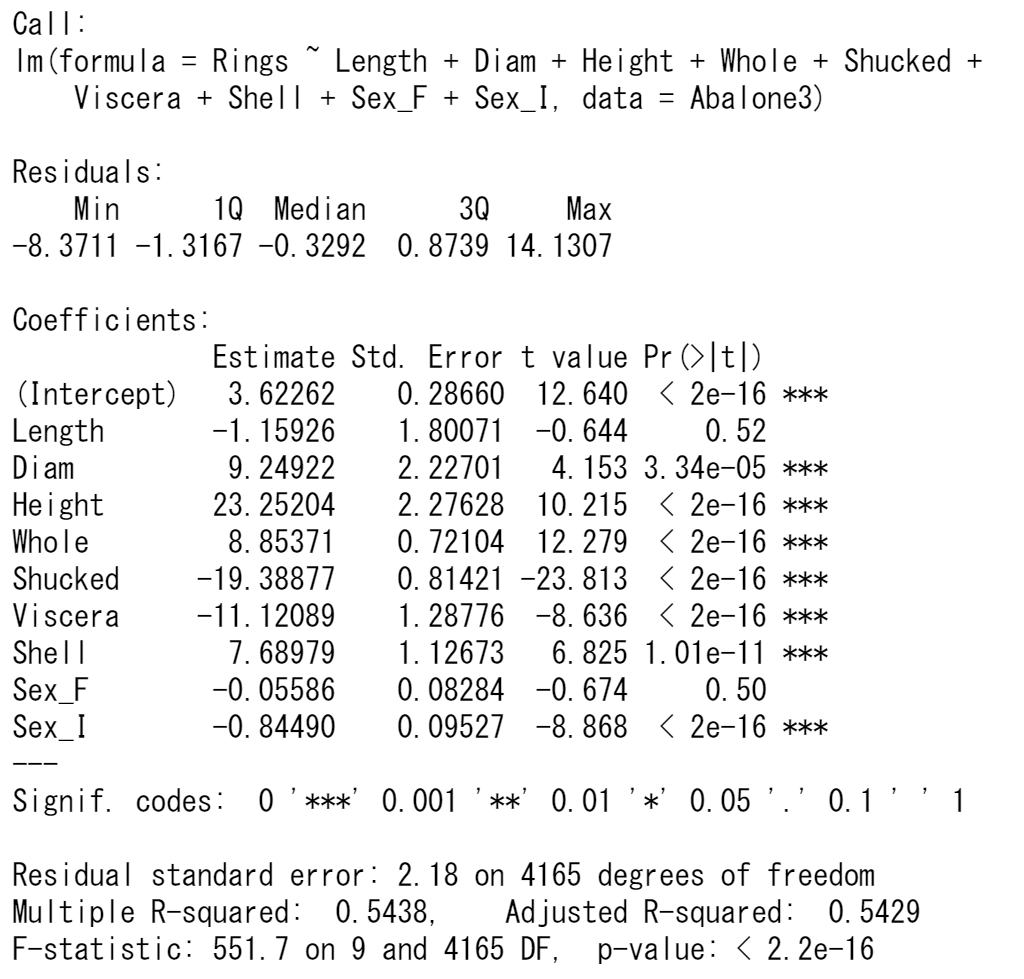
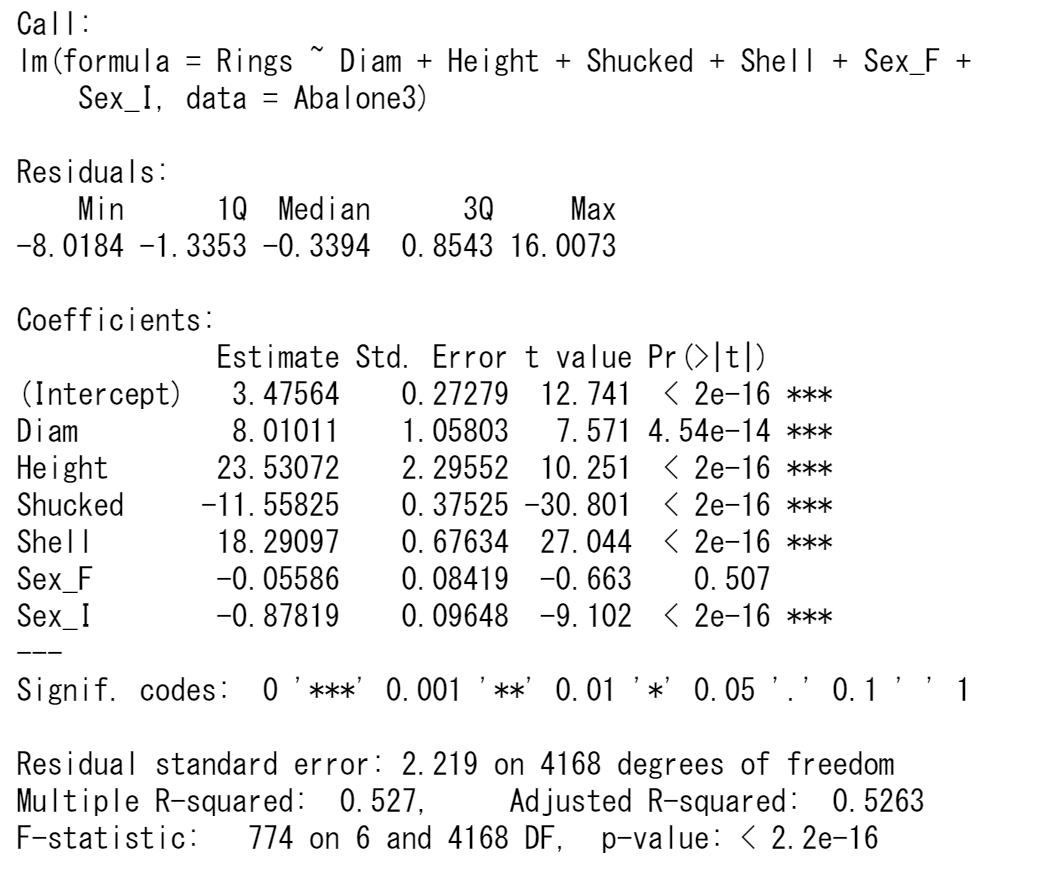
検定結果が有意になった説明変数だけにして、回帰モデルを推定しなおします。
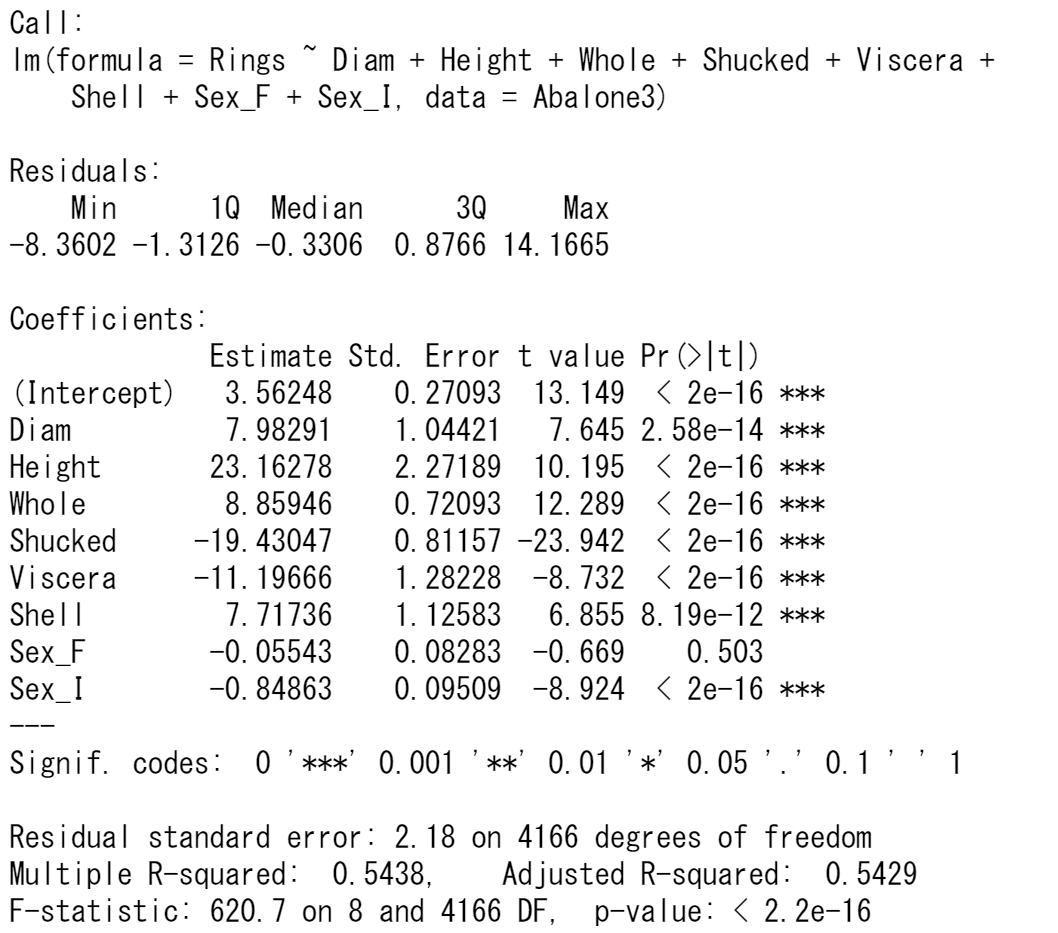
残差についてのプロット図を見てみます。
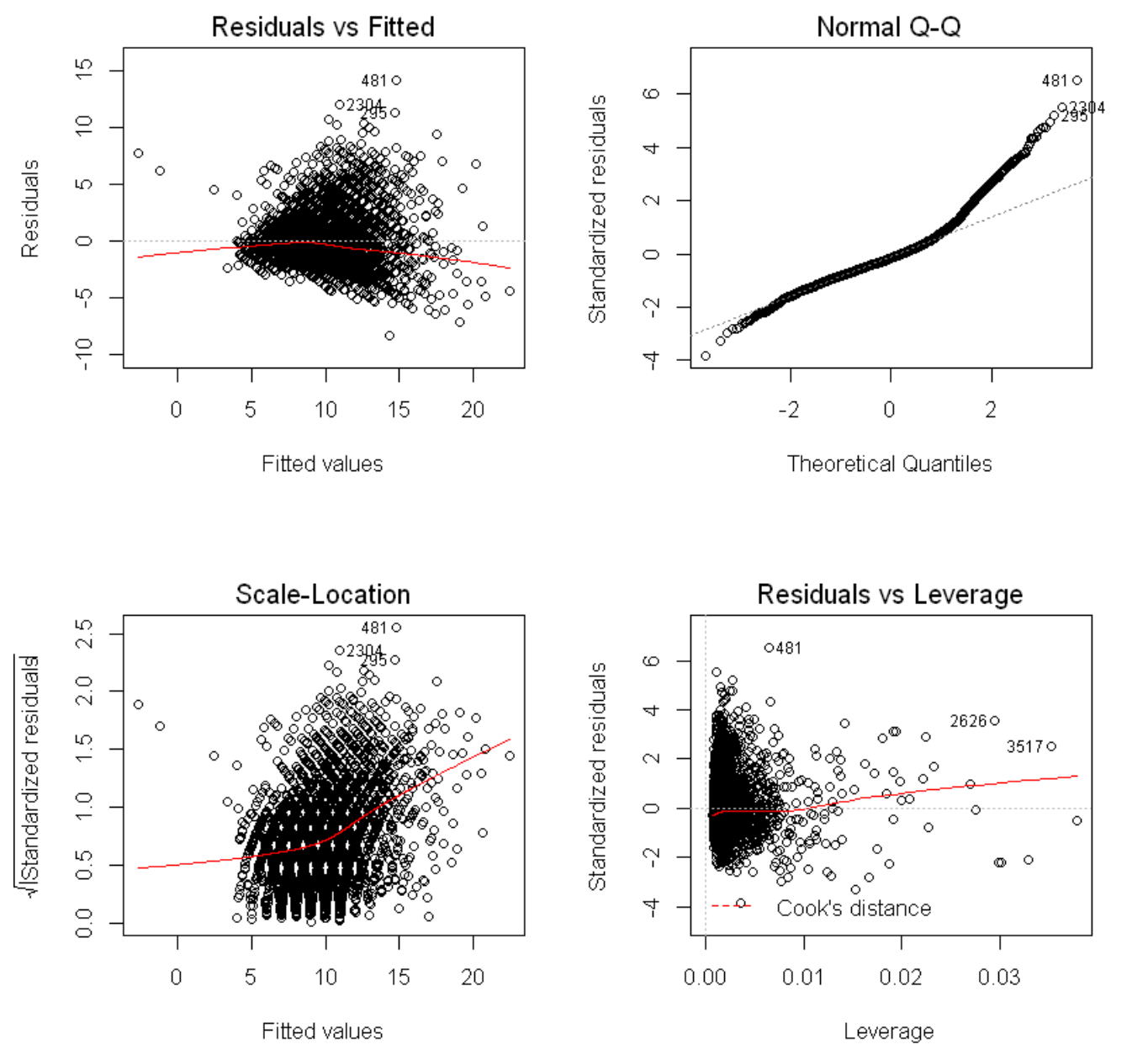
VIFを見ます。
VIFの一番大きな値のWholeを除いて、回帰モデルを推定しなおします。

1個の変数を除いただけでも、VIFは問題がなくなりました。
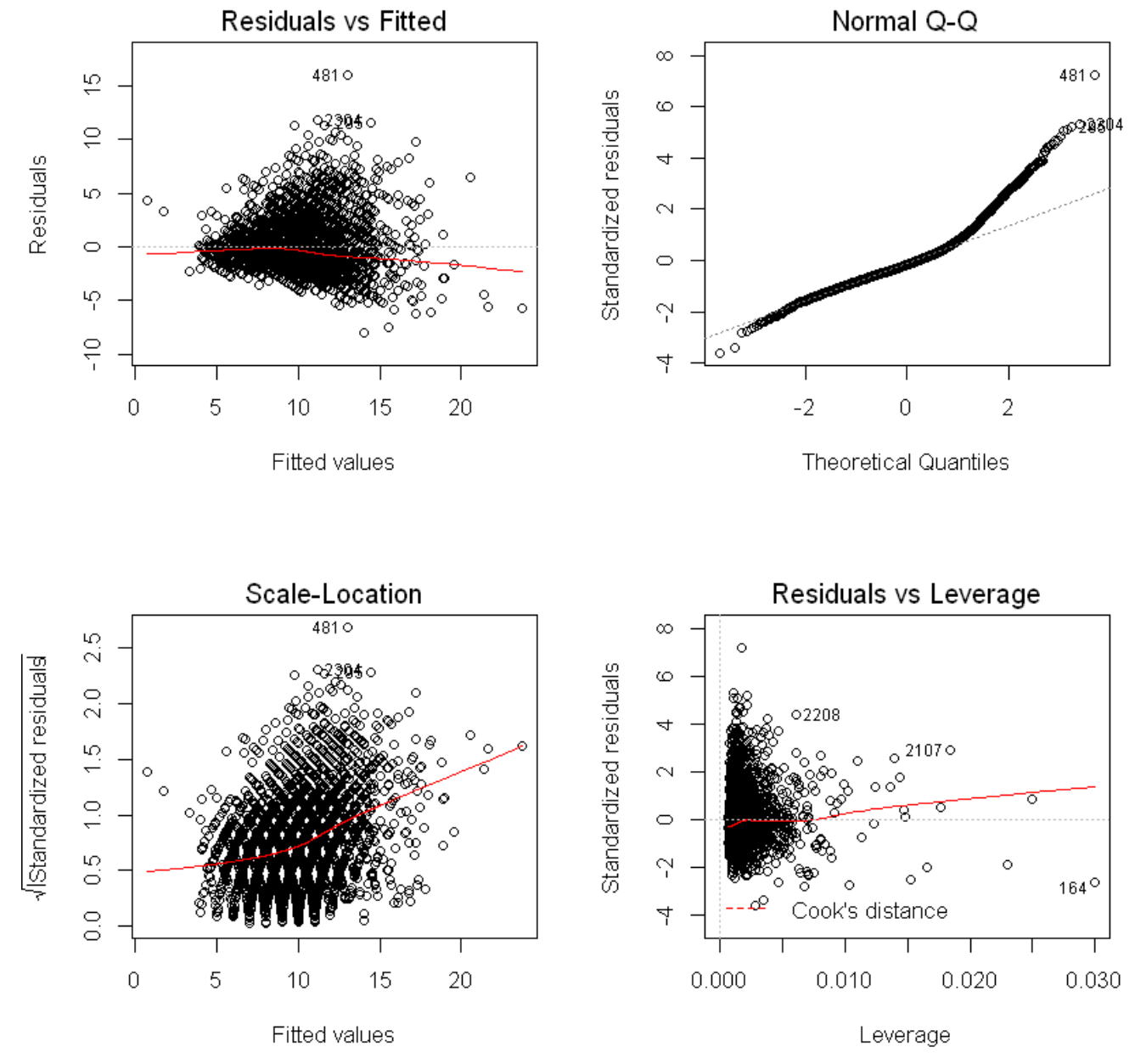
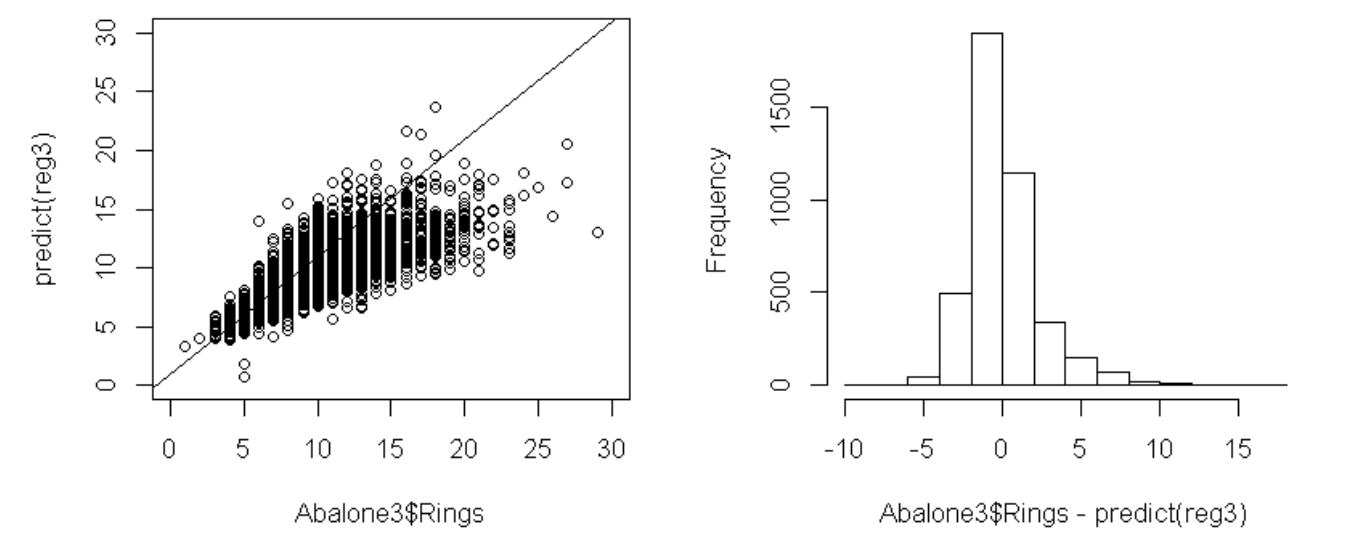
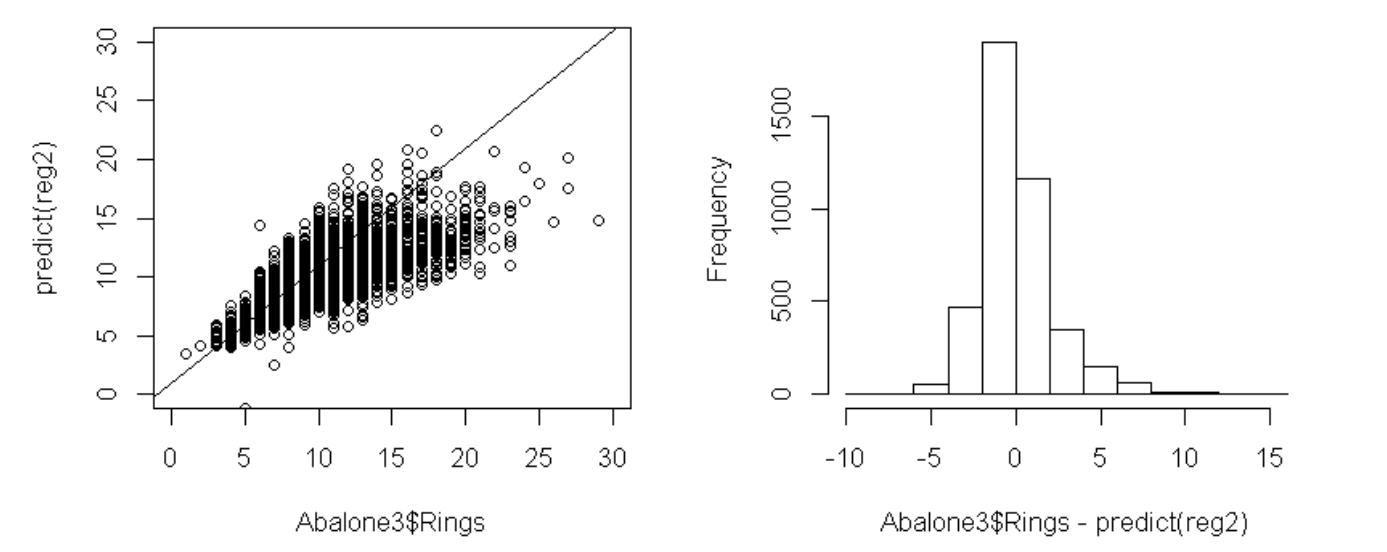
左下の目的変数Ringsと目的変数の予測値のグラフを見ると、Ringsが25より大きな観測値の影響があるようですので、これらの観測値(4個)を外して回帰モデルを推定してみます。
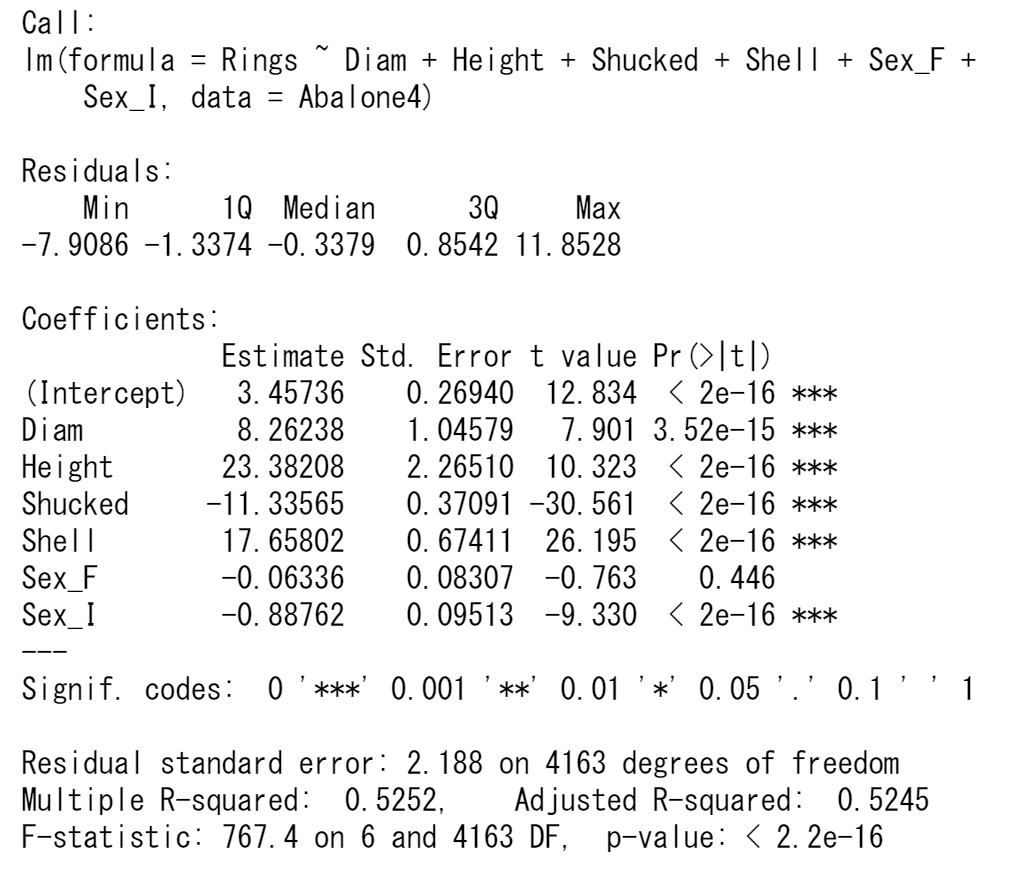
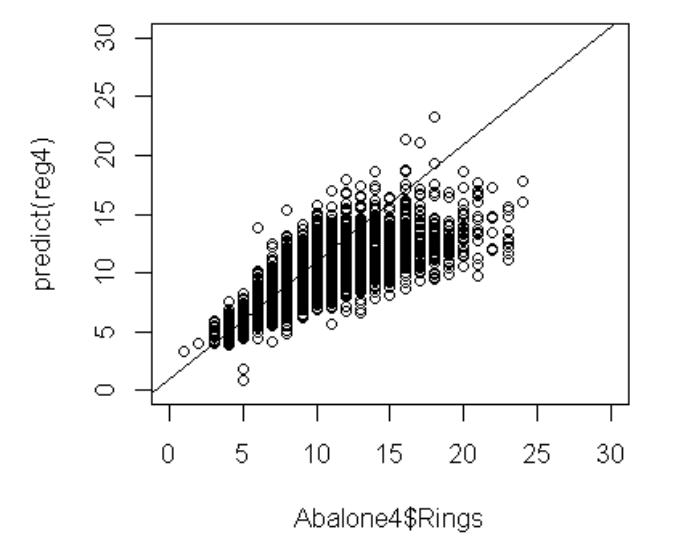
決定係数は0.5252(重相関係数は0.7247)です。
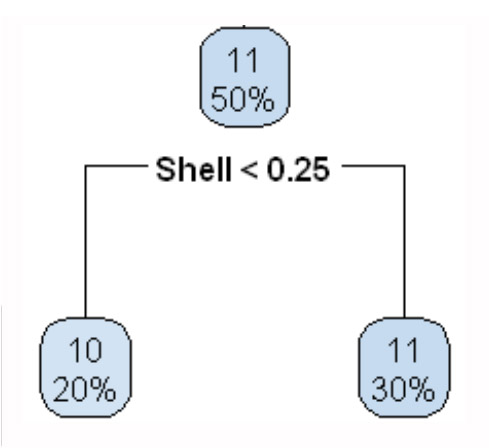
決定木はラベルつきデータ(x1,y1),…., (xn,yn),が観測されたとき、木構造の推論規則を用いて入力xに対するラベルyを予測します。ここで、木構造とは下図のように枝分かれしていくグラフ構造を指します。
データx=(x1,…,xn)∈Rdに対して、根ノードから出発し、各ノードにある条件に従って葉に向かって進んでいきます。葉に割り当てられたラベルがxに対する予測値です。各ノードでの条件は、典型的には、x∈Rdのある要素xk (k∈{1,….,d})と実数cに対して「xk>cを満たすかどうか」という形式で記述されます。この条件に従って、次に進むノードが決まります。すなわち、xの各要素に対するif-thenルールの組み合わせによって、最終的なラベル予測を行います。このような推論規則を決定木(もしくは分類木)といいます。
決定木の学習では、判別、回帰の両方の問題に対してほとんど同じアルゴリズムを適用できるため、汎用的な手法として広く用いられています。さらに、各ノードで単純なルールに従って入力空間が分割されるため、学習された規則を解釈しやすいという利点があります。一方、予測精度はあまり高くありません。
参考文献:金森敬文、Rによる機械学習入門、オーム社
ここでは、連続量であるリングRingを目的変数として、決定木による回帰を行います。

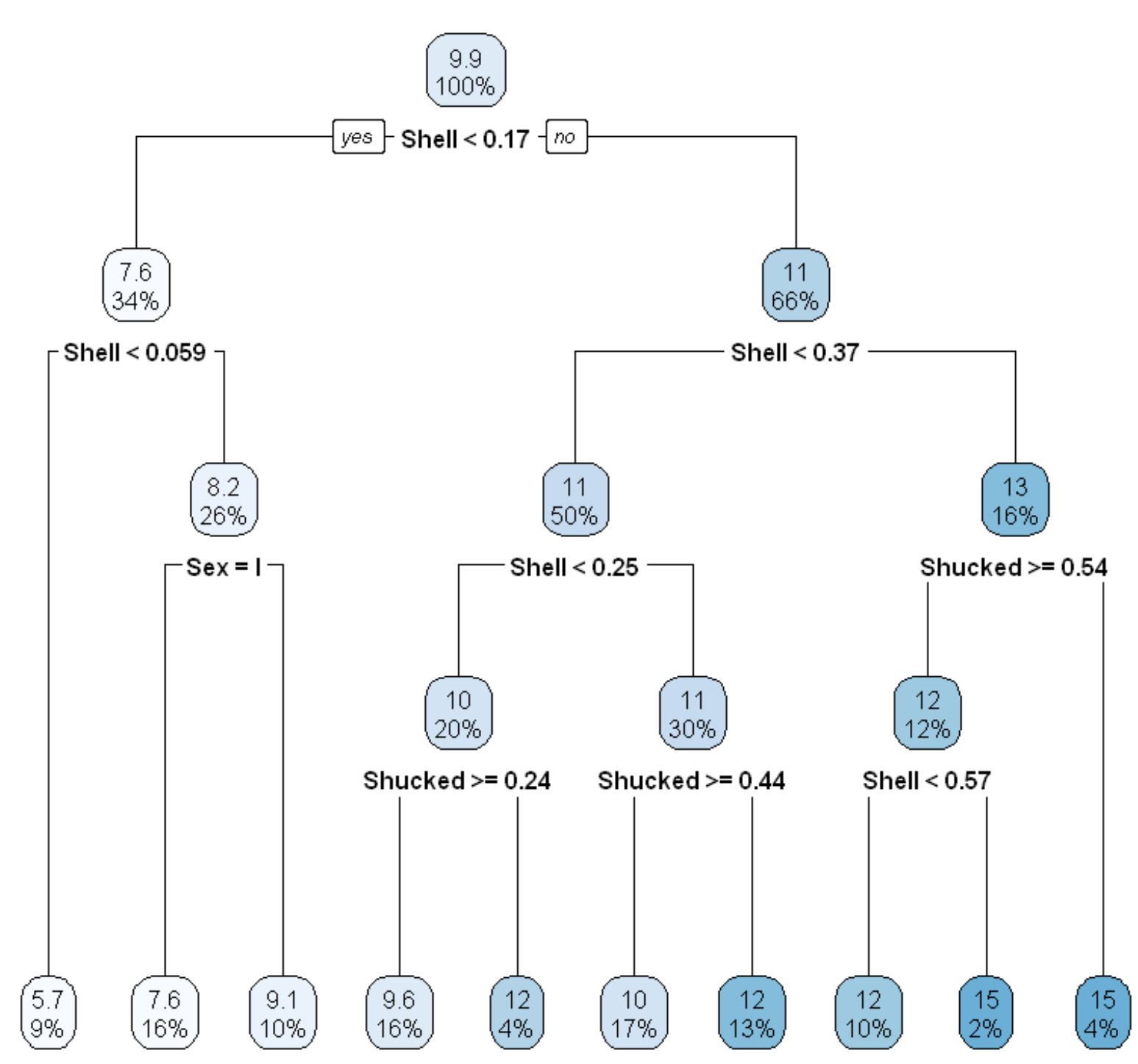
決定木による目的変数の予測値と目的変数との相関係数は
0.69108
となりました。
ランダムフォレストは、データの特徴量(説明変数)をランダムに選択して決定木を構築する処理を複数回繰り返し、各木の推定結果の多数決や平均値により分類・回帰を行う手法です。ランダムに選択されたサンプルと特徴量(説明変数)のデータをブートストラップデータと呼びます。ランダムフォレストは決定木のアンサンブル(集合)であり、このように複数の学習器を用いた学習方法をアンサンブル学習とよびます。
参考文献:寺田学ほか、Pythonによるデータ分析の教科書、翔泳社
ここでは、連続量であるリングRingを目的変数として、ランダムフォレストによる回帰を行います。

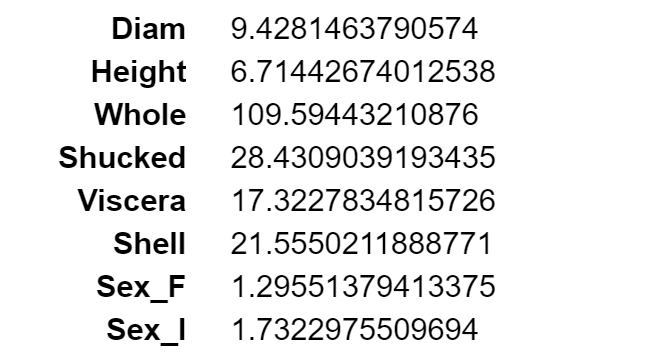
説明変数の重要度は以下のとおりです。
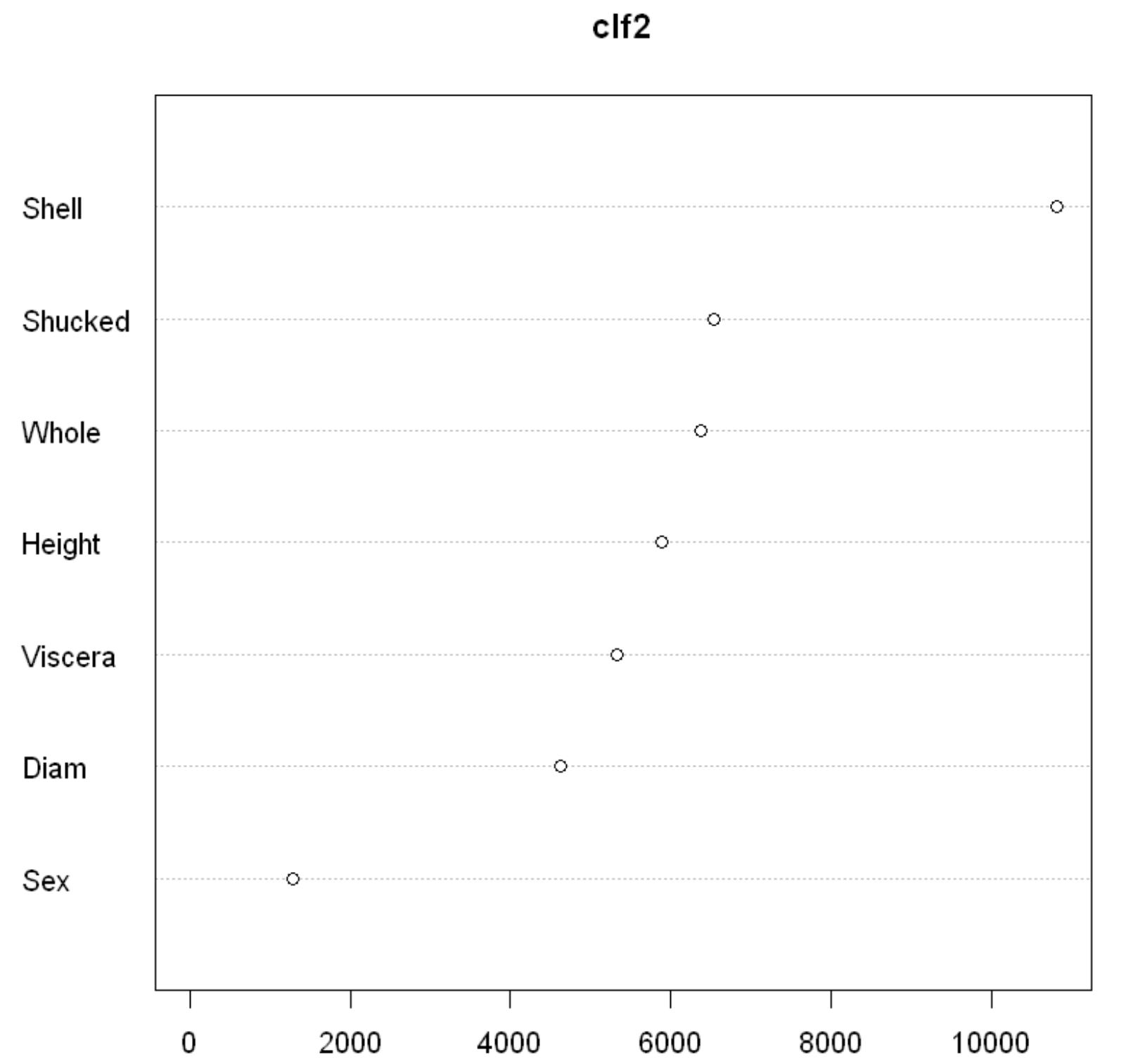
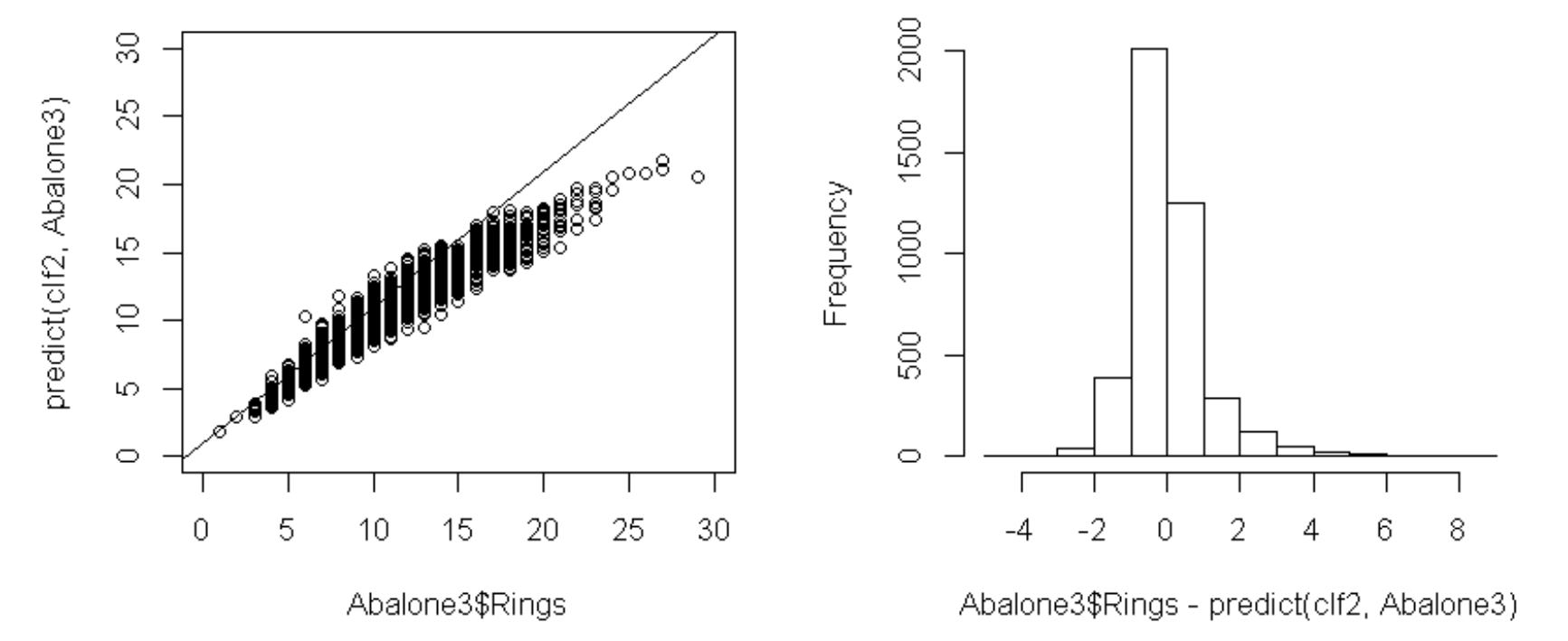
ランダムフォレストによる目的変数の予測値と目的変数との相関係数は
0.95826
となり、予測精度が高くなりました。目的変数の予測値と目的変数の散布図を見ても、よくフィットしていることが分かります。
つぎに、学習データとテストデータに分けて、学習データで作成したモデルがテストデータで精度よく予測できるかどうか確認してみます。以下のように分けます。
学習データ:3131
テストデータ:1044

ランダムフォレストの学習データとテストデータそれぞれの場合の相関係数(目的変数の予測値と目的変数)は以下のとおりです。
学習データ:0.95778
テストデータ:0.74630
目的変数の予測値と目的変数の散布図は以下のようになります。
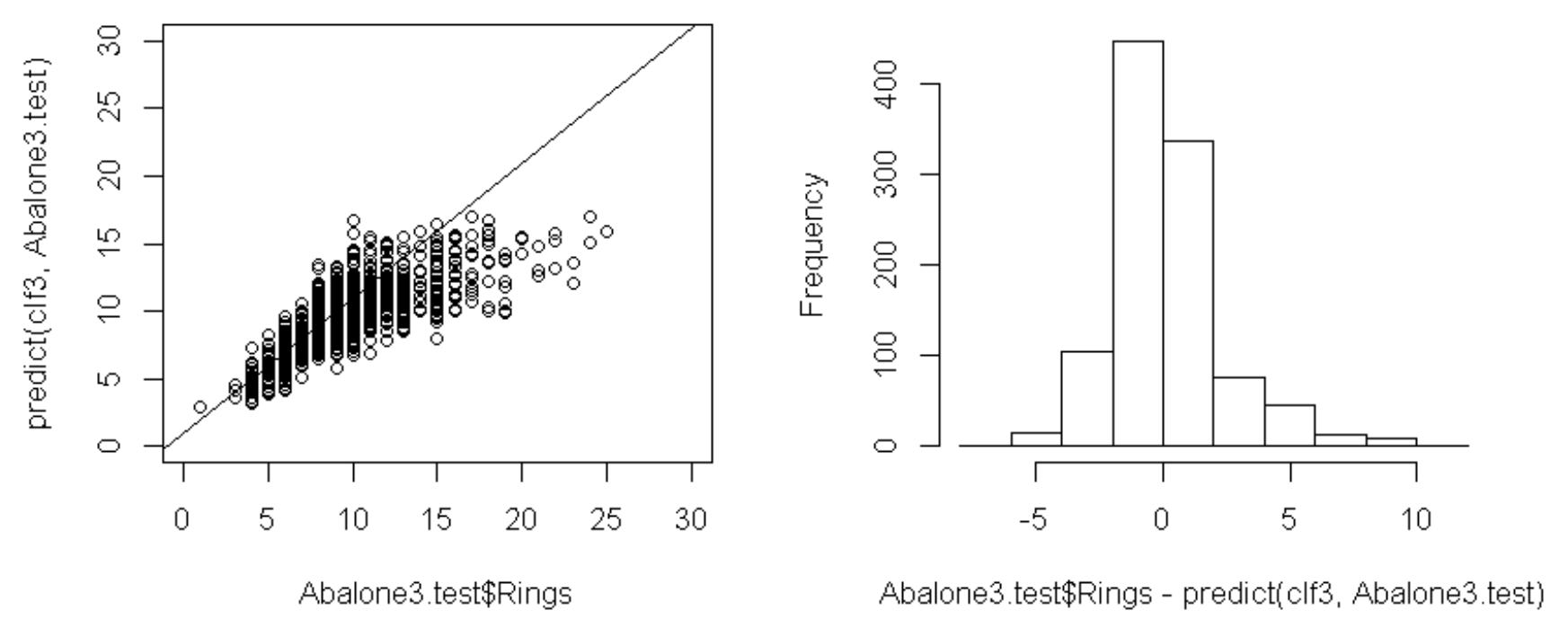
abalone01_python.html
abalone01_R.html
スクリプトと結果は一部分です。全体はセミナーのときに紹介します。
Copyright © 2019 株式会社スタットラボ All Rights Reserved.《Web Design:Template-Party》